CMPUT 307 – Lab 6
Principal Component Analysis (PCA)
主成分分析代写 In this lab you have to implement the Principal Component Analysis (PCA) algorithm and apply it on the provided 2D (eclipse1.mat, eclipse2…
In this lab you have to implement the Principal Component Analysis (PCA) algorithm and apply it on the provided 2D (eclipse1.mat, eclipse2.mat and eclipse3.mat) and 3D data (3d_sphere.mat, teapot.mat and bun_zipper.mat) respectively.
Figure 1 shows an example of the expected visualization results on the synthetic 3D sphere, teapot and bunny used for this exercise.
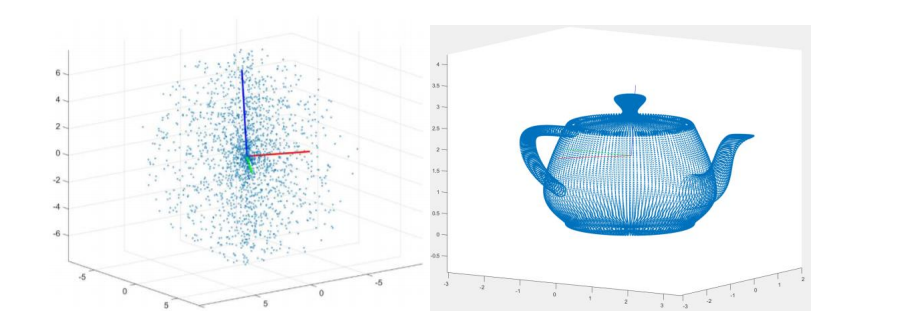
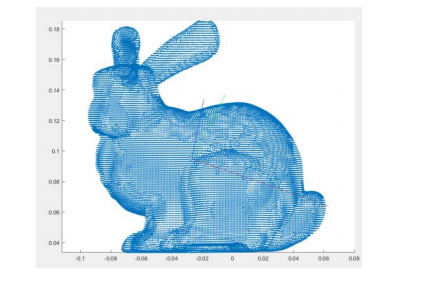
Fig 1. Visualization of sphere, teapot and bunny after applying different 3D transformations. 主成分分析代写
The skeleton code for this exercise will not be provided and you are required to implement the complete code from scratch satisfying the following requirements:
- Finish a function “center”, which, given N samples of data X in d-dimension, calculates the mean/centroid of data X along the d-axis and returns the centered data X_centered and the centroid.
- Finish the main “PCA” function which takes data X in shape (N, d). It returns the covariance matrix, eigenvalues and the eigenvectors computed by the PCA.
- Finish two functions plot2d _pca and plot3d _pca which plot the data and the principal components in 2D and 3D respectively. Notes:
(1) For the 2D data, mark the first and second components with blue and red, respectively. For the 3D data, mark the first, second and the third components with blue, red and green, respectively. 主成分分析代写
(2) A good practice is to scale the principal component with its variance. Think carefully how you should plot the principal components to achieve a good visualization.
Submit a zip file with all your codes used during this lab, including a .pdf file with a table reporting the eigen values and eigen vectors corresponding to each of the 2D and 3D data files.



