MT3852
图灵机代考 nswer THREE questions from FOUR The number in square brackets shows the maximum marks obtainable for that question or part-question.
MODULE TITLE:
Automata, Languages and Complexity
EXAM DURATION:
2 hours
EXAM INSTRUCTIONS: 图灵机代考
Answer THREE questions from FOUR
The number in square brackets shows the maximum marks obtainable for that question or part-question.
Your answers should contain the full working required to justify your solutions.
Each question is worth 20 marks
PERMITTED MATERIALS: Non-programmable calculator
YOU MUST HAND IN THIS EXAM PAPER AT THE END OF THE EXAM.
PLEASE DO NOT TURN OVER THIS EXAM PAPER UNTIL YOU ARE INSTRUCTED TO DO SO.
This question is on regular and context-free languages. You may use results from lectures, provided that they are clearly stated.
(a) State the formal defifinition of a non-deterministic fifinite state automaton.
[3]
(b) Consider the regular expression R = a∗(b(a + b)∗ab)∗ . Give a (diagram of a) DFA that accepts the language L(R).
[3]
(c) Is the language 图灵机代考
L1 = {w ∈ {0, 1}∗ : w contains twice as many 0s as 1s} regular? Justify your answer.
[2]
(d) Consider the language
L2 = {w ∈ {a, b}∗ : w starts and fifinishes with the same letter, and has length a multiple of 3}.
Give a context-free grammar that generates L2.
[3]
(e) For each of the following two languages, either give a (diagram of a) PDA accepting it, or a proof that it is not context free.
(i) L3 = {anb3n : n ≥ 1}.
(ii) L4 = {anbnan : n ≥ 0}.
[5]
(f) Show, by giving an example, that the intersection of two context-free languages may not be context free. Justify your answer.
[4]
This question is on Turing machines and decidability. You may use results from lectures, provided that they are clearly stated.
(a) State the formal defifinition of a Turing machine. 图灵机代考
[3]
(b) Give an implementation-level description of a Turing machine to recognise the language
L1 = {1i#1i2 : i > 0}.
[You do not need to give a formal specifification of your Turing machine.]
[6]
(c) Show that if L2 and L3 are Turing recognisable, then so is
L2L3 = {w1w2 : w1 ∈ L2, w2 ∈ L3}.
[4]
(d) For each of the following languages, state whether it is Turing decidable. Justify your answer in each case.
(i) L4 = {hMi : M does not accept any word of odd length}.
(ii) L5 = {hMi : M halts after at most 50 steps, on every input word w}.
(iii) L6 = {hDi : D is a DFA that accepts at most 50 words}.
[7]
This question is on Complexity Classes and Satisfifiability problems. 图灵机代考
(a) Are the following inclusion relations known to be true, known to be false, or unknown?
- P is a strict subset of co−NP;
- NP is a subset of co−NP;
- co−NP is a strict subset of P;
- PSPACE is a subset of EXP;
- EXP is a strict subset of PSPACE; and
- P is a strict subset of PSPACE.
[Note: you do not have to provide justififications.]
[3]
(b) Using the Space Hierarchy Theorem, or otherwise, show that NP is a strict subset of EXPSPACE.
[3]
(c) Show that the complexity class NP is closed under intersection.
[4]
(d) The MAJORITY-SAT problem is formulated as follows:
Given a logical formula in Conjunctive Normal Form, decide if the majority of variable assignments would satisfy the formula. More explicitly, if such a
formula has k variables, decide if there are at least 2k−1 +1 difffferent satisfying variable assignments.
For example, the formula
(a ∨ b) ∧ c
has three satisfying assignments and is not in MAJORITY-SAT, but the formula
(a ∨ b) ∧ (a ∨ c)
has fifive satisfying assignments and is in MAJORITY-SAT.
Show that the MAJORITY-SAT problem is in PSPACE.
[4]
(e) The FOURSOLUTION-SAT problem is formulated as follows: 图灵机代考
Given a logical formula in Conjunctive Normal Form, decide if there are at least four difffferent satisfying variable assignments.
For example, the formula
(a ∨ b) ∧ (¬a ∨ b) ∧ c
has only two satisfying assignments, but the formula
(a ∨ ¬a ∨ b) ∧ c
has four.
Show that FOURSOLUTION-SAT is NP-hard. You may assume NP-hardness of problems mentioned explicitly in lectures or tutorials, provided you explicitly state which problem you are so considering.
[6]
This question is on algorithms and their complexity.
(a) For each of the following recurrences, use the Master Theorem to solve it for the asymptotic growth of T(n), or explain why the Master Theorem does not apply:
(i) T(n) = 8T(n/2) + n3 log n
[2]
(ii) T(n) = 8T(n/2) + n2 log n
[2]
(iii) T(n) = 8T(n/2) + n2 (3 − 2 cos n) log n
[2]
(iv) T(n) = 8T(n/2) + n4 (3 − 2 cos n) log n 图灵机代考
[2]
(b) Assume for this question we are working with directed graphs G = (V, E). Graphs are given as input in a standard representation: a list of vertices and a list of edges.
A path P between two distinct vertices s and t, both in G, is a nonempty alternating sequence of vertices and edges starting and ending with vertices
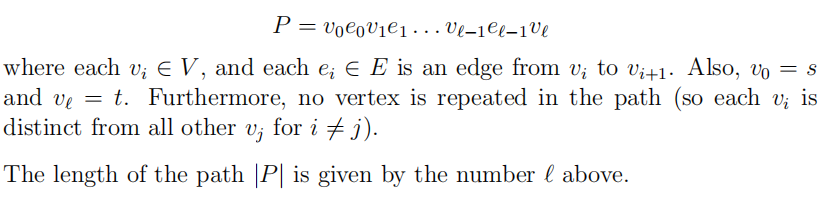
(i) Consider the decision problem where the input is a directed graph G = (V, E) as above, two vertices s and t in V , and a natural number k > 0, and the output is whether or not there is a path from s to t of length ≤ k. Show that this problem is in P.
[4]
(ii) Consider the decision problem where the input is a directed graph G = (V, E) as above, two vertices s and t in V and a natural number k > 0, and the output is whether or not there is a path from s to t of length ≥ k. Show that this problem is in NP.
[3]
(iii) Consider the same decision problem as in Question 4(b)(ii). Show that this decision problem is NP-hard. You may assume NP-hardness of problems mentioned explicitly in lectures or tutorials, provided you explicitly state which problem you are so considering.
[5]



