FIN 322 McKeever

Homework代写 Now, let’s assume that there is a risk-free asset that returns the risk-free rate , and that the maximum Sharpe ratio
Homework #2 – due Wednesday, November 7th, in class
1)Two-Asset Portfolio Choice (3 points each) Homework代写
a)Two risky assets, A and B, have identical return volatilities . Prove that, for any correlation , a two-asset portfolio combining A and B with weights and is minimally-risky when the weights are .
Answer:
The volatility of the portfolio is
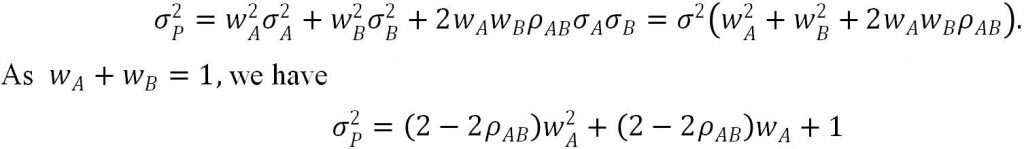
Due to
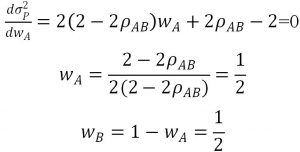
Besides,
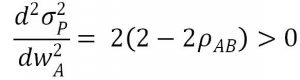
Thus, the portfolio is minimally-risky when the weights of A and B are equal to 0.5.
b)Two risky assets, A and B, have positive return volatilities and , with . Homework代写
If , show that the weights and that would achieve a riskless portfolio are in inverse proportion to the asset volatilities and .
Answer:
The volatility of the portfolio is
![]()
Riskless portfolio means that , Thus we have
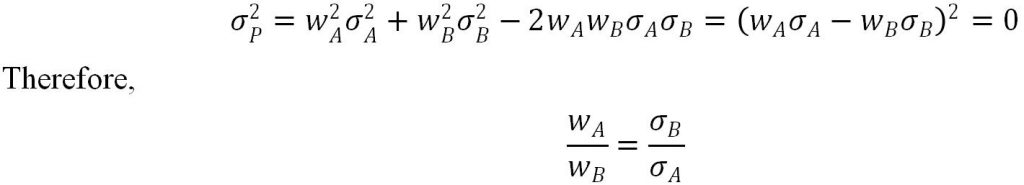
2)The Efficient Frontier (3 points each) Homework代写
a)An investor has the utility function ![]() , where is the expected return on the portfolio and is the portfolio variance. The efficient frontier (with no risk-free asset) is given by
, where is the expected return on the portfolio and is the portfolio variance. The efficient frontier (with no risk-free asset) is given by 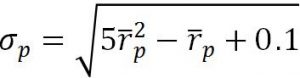 . Find the risk and expected return of the efficient portfolio that this investor will choose to maximize his or her utility. (Hint: write the investor’s utility function in terms of , then find its maximum.)
. Find the risk and expected return of the efficient portfolio that this investor will choose to maximize his or her utility. (Hint: write the investor’s utility function in terms of , then find its maximum.)
Answer:
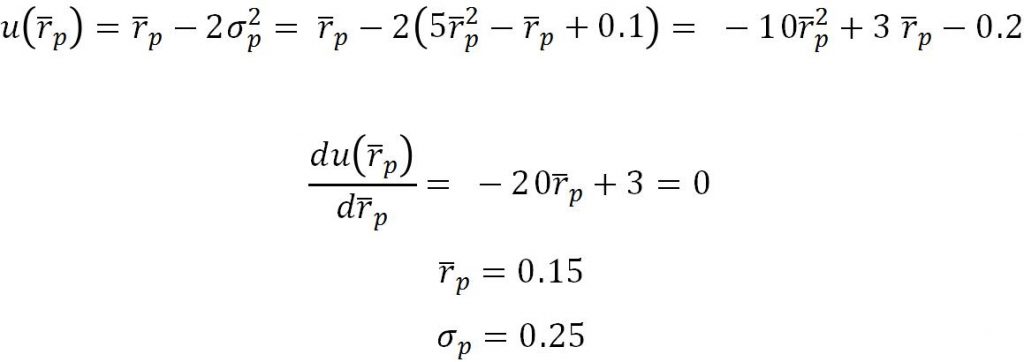
Besides,
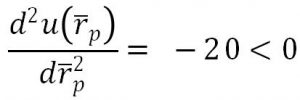
Thus, ![]() , is when the investor will choose to maximizer his utility.
, is when the investor will choose to maximizer his utility.

Answer:
According to
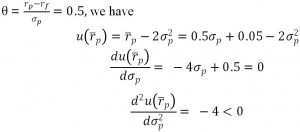
Thus,
![]()
For the portfolio , the utility is
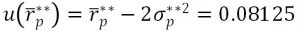
For the portfolio , the utility is
![]()
Thus,
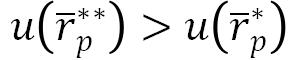
c)Find the expected return and the risk of the tangency portfolio, using the efficient frontier and the CAL from parts (a) and (b) of the question. (Hint: recall that the tangency portfolio is the unique portfolio that lies on both the CAL and the efficient frontier.)
Answer:
According to
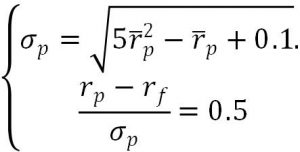
Thus
![]() Homework代写
Homework代写
d)Graph the efficient frontier, the CAL, and the indifference curves that correspond to the investment portfolios chosen by the investor in (a) and (b), and attach the graph to your homework. You can use the graphing calculator on desmos.com, Excel, or some other method. (Hint: for graphing the indifference curves, plug in the utility function values for each portfolio, then rearrange to get by itself on one side as the dependent variable.) Then, answer these questions:
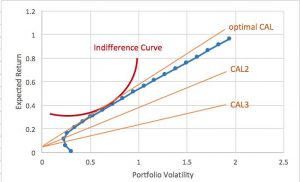
(Please refer to the sheet2 of “HW2.xlsx”)
-Dropping the risk-free asset causes the investor’s portfolio to move “down” the “hill of happiness” (i.e., they get less utility from the portfolio with no risk-free asset). Can you explain this result in the context of constrained optimization?
Answer: Homework代写
The tangency portfolio lies on the intersection of the CAL which is tangent to the efficient frontier (namely optimal CAL) and the efficient frontier, thus under the same utility, this is the portfolio with highest expected return per unit of the risk. When drop the risk-free asset, in order to make the indifference curve insect with the efficient frontier, it must move down, causing less utility.
-What are the portfolio weights on the risk-free asset and the tangency portfolio in portfolio ? Explain the portfolio strategy in terms of borrowing or lending.
Answer:

We can achieve higher expected return by borrowing at the risk-free rate and investing the proceeds in the risk asset.
3)Portfolio Optimization in Excel (7 points) Homework代写
Download the file “HW2.xlsx” from Blackboard. For all problems, assume limitless borrowing and lending at the risk-free rate, and no restrictions on short-selling. The risk-free rate is 10%.
a)Create the expected return vector and the covariance matrix from the data provided (ten years’ worth of annual returns for four fictional stocks: ABC, DEF, GHI, and JKL). Use the arithmetic average of returns for expected returns. Use the COVAR command or the Covariance tool in Data Analysis to create the covariance matrix.
b)Find the weights of the tangency portfolio. To do this, you’ll need to construct the summing vector and the matrix . You’ll also need to find the values of the constants A, B, and C (see class notes). Use Excel command MINVERSE to construct the inverse covariance matrix. Use Excel command MMULT to multiply the relevant vectors and matrices.
c)Find the expected rate of return on the tangency portfolio and the risk of the tangency portfolio . Then, plug these in to the expression for the efficient frontier to prove that the tangency portfolio is in fact on the efficient frontier.

更多其他:Resume代写 Report代写 Proposal代写 Capstone Projects 润色修改 代写案例 Assignment代写 助学金申请 成品购买



您必须登录才能发表评论。