MATH 187A Introduction to Cryptography
HOMEWORK 4
密码学入门代写 Instructions. You can collaborate with up to two other students on the homework. Problems should be solved together, not divided…
Instructions. You can collaborate with up to two other students on the homework. Problems should be solved together, not divided up between partners. You must write the solutions on your own in your own words, though and mention your collaborators.
Homework must be submitted through Gradescope by 11:59pm PST on the due date, and there are no exceptions to this rule.
You will be able to look at your scanned work before submitting it. Please ensure that your submission is legible (neatly written and not too faint) or your homework may not be graded. By turning in your work, you acknowledge that the work contained in the document is your own and you did not engage in any academic misconduct. After uploading, indicate which problems are on which pages on Gradescope.
Students should consult the class notes, lecture slides, instructor, and TAs when they need help with homework. Students should not look for answers to homework problems in other texts or sources, including the internet. You may ask questions about the homework in offiffiffice hours and on Zulip. However, you should only use Zulip to ask for clarififications on the homework problems. Publicly posting any part of your work on Zulip or anywhere else will be considered cheating, and the author of the post will fail the class immediately!
Your assignments in this class will be evaluated not only on the correctness of your answers, but on your ability to present your ideas clearly and logically. You should always explain how you arrived at your conclusions and justify your answers with mathematically sound reasoning. Whether you use formal proof techniques or write a more informal argument for why something is true, your answers should always be well-supported. Your goal should be to convince the reader that your results and methods are sound.
All problems have equal weight unless otherwise specifified and use the conventions from lecture. 密码学入门代写
Key concepts: chi square statistics, codebreaking for monoalphabetic cipher, rectangular transposition, and Vigen`ere ciphers, entropy, conditional entropy, comma-free code, Huffffman tree, random cryptographic systems, perfect secrecy.
- (5 points) Suppose we use the applet for breaking rectangular transposition and obtain the following matrix under the “Break” page:
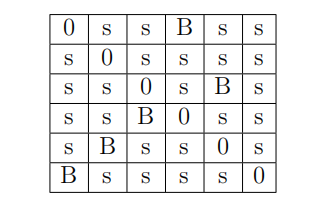
Here, s denotes a small number and B denotes a substantially bigger number on each row/column. Find the decrypting permutation.
For the following three problems, use the corresponding applets available online at the class website (https://www.math.ucsd.edu/~alina/187a/lectureb) to decipher the ciphertexts. Make sure you use the ones marked “new version 1”.
When you decrypt the messages, you must turn them into plain English – that is, you need to put in spacing and punctuation. (The original texts are well known.) Small errors are ok when there are options, but do your best to have a message that really makes sense. Your answers to these three questions must be typed.
-
The following message was encrypted using rectangular transposition. 密码学入门代写
V DIAA HEMAR AHET E Y T NAO DST T I AHNW L INLOI EARSP IUION LEDV H RUT T T EEIUM NEAF S NOT GI EECEW RDDEH LHOT R HST T E UBESO ST EV E LEDF I HANT T T AERL MALNE EERT C AUIDQ LEAER HV DAA T T EMA AHDOO EY NAE DNHET RLF HL OISRA GOIEG SST EN HOOEO FMF RA SRLES V T SAD ENHOO OSF NF RAREL MSW RV OEENL ESIBW LESAL OBT OT IDNTW T ROEE GHHAA T T T EO RBEBL F EOOH HT RHE OIV DA ET ARM DAODH T EANV T AENY ET EHS T EAII OMSF S P ASII SP TW S AST EE NET IL RT HGI TW HAF EEOHT UIIJT NSW T C SLEEN IEIW R GHET T HHEF P AOP T O SNRSO EILTW LEIBS RRNOA F IOMD T ENAS AOINS RDOF E F ENUO AJMDC HSIIT EAEAE RV DHM AT TMA UIY OL F REIT LHT CE ILRW D NNALO DLEV N Y IILE T NAAO NIRHW ET HEI NEW LY LEDOB UT JBH GDT EY LOEOR COESF HRT IB BKNT I UENY H OT CT T T NF EO RAHIH ECT IR CRAEE RHV DA AT AEM DAOAA Y HEIV AHDET RMNAA ODT EW NY OID NBAAA MLAHS W T T II ISV CU IOISR CT ASH SW T T I IEOGV NORV G RANHI LSHSP IIP ND IIRP T HGITW HROEO SW DT P F NRIE T NOIO SINLA DLNUC IIIT F ANAOO DNEGT Y IT RH EAHRN EIALL BAAML LIT BT EBSAK Y COBC ADANL RWKIS GLBBI LALEO ILT OE JNW NA SHDLT IHT T I HELW T EISDB Y NOAT IW IGH EAIRS SLSRN SEAT S OEDRH BTHER IV SAE T ARMD AY AOA HDIDA V AEER ANMHO T T Y EE AV DEA ERV LY LABY H LSLAE EXT EL DEDNV AEIAR HLY LO T NMND USLAN AIHME LEDBA T RLW E OHHAO GLUPW LCSLE IAP BM EEDND LINAA COT EO HRP CK DAELI BEW LS LDT EA SMEGA RIT AH HLNT G DEOHO Y T RF R HEOSL DBEAL RLELA V ADEE LLNAF DLSLE HASHE T LET S IT ROE EGH
(a) (3 points) Is the diagram on the “break” page representing the decryption or encryption permutation?
(b) (3 points) What was the permutation used to encrypt the message? (After you hit “decrypt”, this will show up)
(c) (9 points) Decrypt the message. The answer should look like English and include punctuation.
-
The following message was encrypted using a monoalphabetic substitution.
sjocj ostzi mozzo ijoso ceivs cejoj tddhc evejo fheuj ocejo etydo stztd xvzej hiioc yocot ejtdd iwido rzyhm ejitr bmozo cezhe dvvfo itzej vwkji widor jtikv eeoce jocos uvxbw eomjo stceo icvee vxoce hvcej ozouv cieod oqhzh vctci ejomt uhcky hfooa tuedr sjriw idors tceoi tmtuh ckyhf ostzt xrzeo mrevj tmmrt ziwid orstz qomrl tetci jteoi oaomu hzowc dozzv luvwm zoheh cqvdq oibwc ujhck zvxoy viriw idorz ltqvm heobw cujhc kytks tzjtm mrywe jouvw dicev leocu teujj hxjtm mrihi cedvv fheyw ejost zqomr ltzeb omjtb zhejt izvxo ejhck evivs hejdh qhckh ctitm fuwby vtmiy wejtm mrjti tdstr zyooc zxtdd tcizf hccrl vmjhz tkojo dvvfo ioqoc zxtdd omtci zfhcc homej tcjom otddr stzyo utwzo tddjo jtiev sotms omovd iudve jozvl iwido rztci iwido rstzt yvwel vwmeh xozyh kkome jtcjo stzjt mmrjt itejh cltuo f cvyy drf co ozydt uf jth mtciy mhkje kmooc orozj osvmo mvwci kdtzz ozjod ievko ejoms hejtd vevlz uveuj etboy outwz ovltd dejoe hxozi widor jtibw cujoi jhxvc ejocv zoejo vcdre jhckj tmmrd hfoit yvwej hzvsc tbbot mtcuo stztq omrej hczut mvcjh zlvmo jotie jtest zzjtb oidhf otyvd evldh kjech ckjoj tijti hetzd vcktz jouvw dimox oxyom tciej olhmz enwoz ehvcj ouvwd ioqom moxox yomtz fhckj hztwc eboew chtst zjvsj ojtik veeoc he
We also know that the plaintext contained the words: 密码学入门代写
DUDLEY P ERHAP S W ANT ED.
(a) (3 points) What did you choose to replace DUDLEY ? What was its chi-square statistic?
(b) (3 points) What did you choose to replace W ANT ED? What was its chi-square statistic?
(c) (9 points) Decrypt the message. The answer should look like English and include punctuation.
- The following message was encrypted using the Vigen`ere cipher.
XCBHV KY XHF ZCICV P BJGL RSDRA W PMBI GUEQG XQV AI ZGV P E RWW RR ISV RD JCY P P IV QY V SNMOS BIBSS XPMSH EW HQS RP RXK GCGBH RW P IA NF JRS XHRQI DARKR AIUY D MBASI Y W IEV GDLCL NF F HC XW HZQ RLOHG BKLT O XRF XL KY RLG SLRCR NGMRL KP Y BC DJDCG UIJPK ZRF SI W Y Y AT EP CBM P NRV U RSNAW ZCBIQ GLHAK P Y GSV CBZV P IV SBV BHRGR RIT Y S ECXSJ GLHRB Y ZCIW QEQZB RV SCE T NMQL Y XNF E F Y V P G BF HY B EEZWW F Y Y T U EUKCA RAIHB XSGNW DAKP Y GSEY D XY RXK MEKUR QEY DX Y RHZC KV ROY W Y MEY Y XRZO EEGLH ZEV QR RRDKP BAKW U SP V T L W QDV H TKOCI INEMQ Y XHLR EUMEX ERNRG MMATM QF Y T R CEW GO RGV RW P SFHY EW GY R NF XUS QKY RE JY SRF GXKCM SZZSQ CXIZV IV MP Q NAXBP KRALT RT OV G LHLQO EF REQ BGEEV XV CV J V AXKC V SAT L LQDSE LSIRR IJBV O BY RY L EICGK RAIUY DMBAW KY F IO RIQEB EAGIG RRIEB P HMP H RSIQB SRT SV HCNSZ V RLRC LBHV R DW EKV QXKNE AT IUG NSABX V F BMA XJUMW XUV W U CCT BA W LZSP V GCLU OP P BQ HGDMQ BRRRL IY V IY CDLNG EQW Y J HF ARS V HRKG KY XKR CP DAO W JV XK Y XCBG LHP ZI BCP HM BEALS W F OV T RRHPK XV BRW F OIAR V JW DL RSELR RXURH HT Y XV BRZF S GUJIE P SRT G SW F SW RAHHY F SHEA LJV P V T LWME V P BY Q RBCNA HDJV A UBW HP F IV GE QBDLR T P RUP V BZXK Y DJV E IF Y XX EHP BJ SKUGX KCGSE Y HDLN W BZCI CV P BJ EP CBM P NRV Y COABX ZFKXL BY UAY Y AGV B AKRQB JRP IS HNW NU REGLS XAKRQ BJRP I SHEGR SXXEL QBDOP Y BAF G DMMRR V MP XU RARP V HNF OQ MDAUN XDKOV V P EZG V P QBJ RP ISH OY W UR EGGSJ CDLRE AHAKR QBJRP DLRSV HCNSZ BJP Y X JV AEO JIAUR XKCBC BHEUC MMGV D HLCSS NQHP S GNBV F GDMMR RV MP X URARP V HNF O RDEW G UIV Y W IUV KK QDEAQ EUBCS SF XUC XKGUE QBCEP EMIGM IJUMF F GINF ORDIS HJMW F KKBBH FMXW P V IQAO SHESQ JIW HE IUCGE EQALR RLV F X RP IXU RJLLK PW HHJ CY JBH V GCOH F Y IW S CKBSS URRXB Y IDBD LRY EQ BGIY B ZHY CO V AKKG CF Y RW V GXKN AHKGC LRY T E SDOAB ALLQX UNXKC BIBAI DP DLT BHV UY V XZY V RDV HY CECY Y EBAQ
(a) (4 points) Find the keyword. 密码学入门代写
(b) (6 points) Decrypt the message. The answer should look like English and include punctuation.
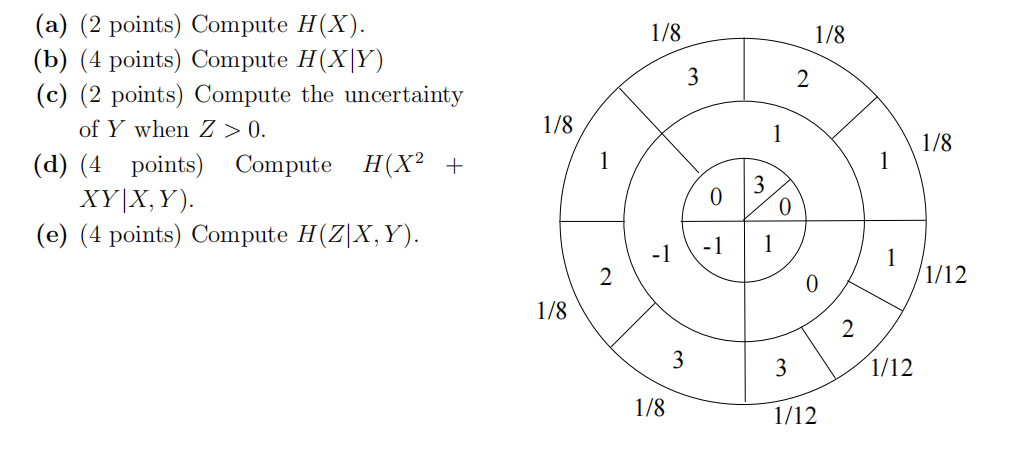
- Suppose that random variables X, Y, Z are obtained by spinning the adjacent wheel, with X given by the outermost circle, Y given by the intermediate circle, and Z given by the innermost circle.
- (a) (Bonus, 3 points) Prove that
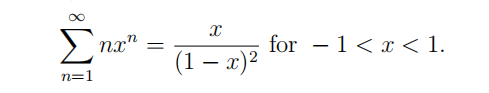
(b) (5 points) Let X be a random variable that takes the values 1, 2, 3, . . . , n, . . . Suppose that for each pxositive integer n
Compute the entropy of X.
Hint: Use the formula from part (a).
-
Suppose a certain fifile contains only these letters with the following frequencies

(a) (6 points) Construct the comma-free code that enables you to compress the fifile so that you can store it using the least number of bits.
(b) (6 points) Use the comma-free code you construct from part (a) to decrypt the following ciphertext.
1 0 0 1 0 1 1 1 1 1 0 1 1 0 0 1 1 0 1 0 0 0 1 1 1 1 1 1 1 0 1 1 0 0
1 1 1 1 0 1 0 0 0 1 0 1 1 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1
0 0 1 1 0 1 1 0 0 1 0 0 1 1 0 0 0 1 1 1 1 1 0 1 0 1 0 1 1 0 1 0 0 1
1 0 1 0 1 0 0 1 1 1 0 1 0 0 0 1 0 1 1 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
0 1 1 0 0 1 0 0 1 1 1 1 1 0 0 1 1 0 1 1 1 0 0 1 0 1 1 1 1 1 0 0 1 1
0 1 1 1 0 1 1 1 1 1 1 0 1 1 1 0 1 0 0 1 0 1 0 0 0 1 1 1 1
-
(Bonus) Suppose a random cryptosystem is obtained as follows: The message consists of two independent random variables X1, X2 each generated by spinning a wheel with arcs labelled 0, 1, both of length 1/2. Let there be 4 equiprobable keys with the following corresponding encrypting transformations: (Draw a picture of the wheel in question if you are confused about the messages.) 密码学入门代写
k1 : (X1, X2) → (X1,(X2 + 1) (mod 2))
k2 : (X1, X2) → ((X1 − 1) (mod 2), X2)
k3 : (X1, X2) → (X2, X1)
k4 : (X1, X2) → ((X2 + 1) (mod 2),(X1 + 1) (mod 2))
(a) (3 points) Does this system achieve perfect secrecy? Explain.
(b) (2 points) What is the probability of receiving the ciphertext 00?
(c) (3 points) Compute H(K|C).
(d) (4 points) Now suppose k1, k3 are chosen with probability 1/8, k2 is chosen with probability 1/4 and k4 is chosen with probability 1/2. What is the probability of receiving each ciphertext? That is, calculate P(C = 00), P(C = 01), P(C = 10), P(C = 11).
(e) (4 points) What is H(K|C) if k1, k3 are chosen with probability 1/8, k2 is chosen with probability 1/4 and k4 is chosen with probability 1/2?



