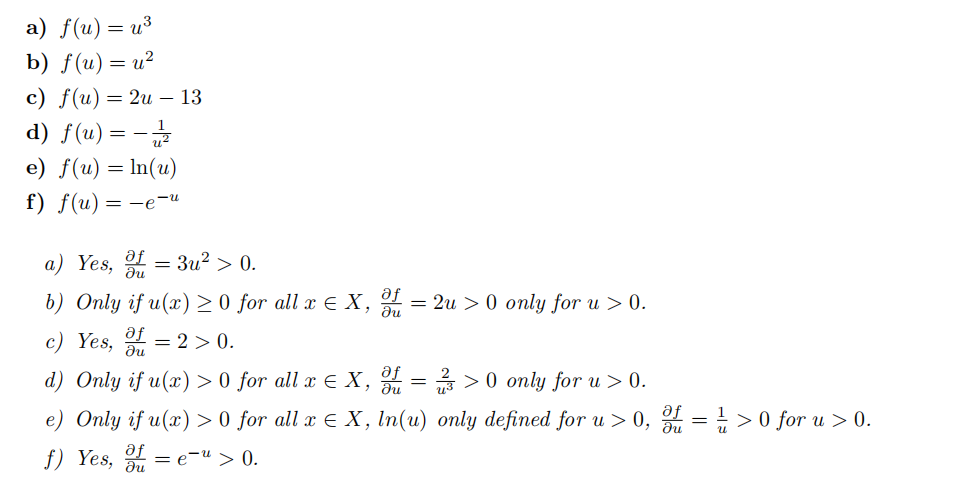BEEM101 Microeconomics
微观经济学代考 Consider a group of people, Alice, Ben, and Clive. Are the following binary relations on the group complete, reflexive, and transitive?
Problem Set 1: Preferences and utility 微观经济学代考
——————————————————————————————————————————–
- Exercise – Properties of binary relations (Varian Ch. 3, RQ 2 and 3)
Consider a group of people, Alice, Ben, and Clive. Are the following binary relations on the group complete, reflexive, and transitive?
a) At least as tall as
b) Strictly taller than
a)
- Complete: For any two people, either person A is at least as tall as person B, or B is at least as tall as A, or both.
- Reflexive: Any person is at least as tall as themselves.
- Transitive: For any three people, if A is at least as tall as B and B is at least as tall as C, then A is at least as tall as C.
b)
- Not complete: Two persons from the group could have the same height and then they could not be ordered according to the strictly taller than relation.
- Not reflexive: No person is strictly taller than themselves.
- Transitive: For any three people, if A is strictly taller than B and B is strictly taller than C, then A is strictly taller than C.
-
Exercise – Properties of binary relations (Varian Ch. 3, RQ 4) 微观经济学代考
A college football coach says that given any two linemen A and B, he always prefers the one who is bigger and faster. Are his preferences complete and transitive?
- Not complete: We cannot compare two linemen where one is bigger but slower than the other.
- Transitive: For any two linemen, if A is bigger and faster than B and B is bigger and faster than C, then A is bigger and faster than C.
- Exercise – Properties of binary relations (OR Ch. 1, P 3)
Consider the following preference formation scheme. An individual has in mind a function v : X → R that attaches a number to each alternative in X. However, she is sensitive only to significant differences in the value of the function. Specifically, she strictly prefers x to y if v(x)−v(y) > 1 and is indifferent between x and y if −1 ≤ v(x) − v(y) ≤ 1. Are the individual’s preferences necessarily transitive?
No, suppose for example v(x) = 1, v(y) = 1.6, and v(z) = 2.1. Then we would have x ∼ y and y ∼ z but z ≻ x.
-
Exercise – Utility representation (OR Ch. 1, P 7)
Let X be the set of all positive integers.
a) An individual prefers the number 8 to all other numbers. Comparing a pair of numbers different from 8 she prefers the higher number. Construct a utility function that represents these preferences.
b) An individual prefers the number 8 to all other numbers. Comparing a pair of numbers different from 8 she prefers the number that is closer to 8. Construct a utility function that represents these preferences.
- a)
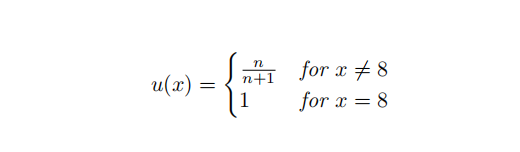
- b) u(x) = −|x − 8|
5.Exercise – Utility representation (Varian Ch. 4, RQ 1 and 2) 微观经济学代考
Suppose u : X → R represents an individual’s preference relation. Which of the following transformations f : R → R can we apply to u such that the function w : X → R defined by w(x) = f(u(x)) represents preferences as well?