Assignment Numerical Methods for EOR
(EBB115A05)
数值方法代写 This assignment is to be completed in the groups that you are assigned to. No changes are permitted at this time.
This assignment is to be completed in the groups that you are assigned to. No changes are permitted at this time.
Please provide the following information on the fifirst page of your solutions: group number as stated on Student Portal and the names and student numbers of members of the group.
Submit your solutions through Student Portal. Please call the fifile that you submit group1.pdf, group2.pdf etc, so that we are not stuck with 33 fifiles each called assignment.pdf
You need to type your answers and include R code in your answers.
You need to show your work and motivate your answers. Simply providing R code without any explanation will not result in full marks even if the code and answer are correct. Explain your reasoning clearly.
Read all the questions carefully and email us if something is not clear.
Answer all 4 questions.
Late submissions will not be graded.
GOOD LUCK!
1. (10 points) Solve the set of nonlinear equations 数值方法代写
3x exp(-y)+exp(y)+z =5
log x + log y + log z =-1
xy +z =2
in (x,y, z)‘.
- (10+10+15+10 points) Consider the data set with daily stock returns that was created in week 1. The dataset to be used in this problem is posted together with this problem set on nestor (don’t use another version).
Important measures in risk management are the Value-at-Risk (VaR) and the expected shortfall. The Value-at-Risk is a level of losses that is not exceeded with large probability. If we denote losses by the random variable L, with distribution function FL.lI /, the Value-at-Risk is defifined formally as

with ∅(.) the distribution function of the standard normal distribution, and ∅(.) the density of the standard normal distribution.
(a) Verify the validity of equations (1) and (2) by means of a simple simulation experiment.
You have seen during the lectures that the tails of the normal distribution are too thin to model daily returns correctly. One alternative is to model the returns according to a normal mixture distribution. The density is given by
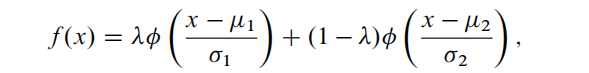
with ∅(.) the standard normal density, and 0 < λ < 1.
(b) Fit normal mixture distribution to the daily returns of the AEX by programming a loglikelihood function and optimizing that function. Estimate all fifive parameters. Report both the point estimates and their standard errors.
(c) Estimate the level of losses that is not exceed with 99% probability using the normal mixture distribution estimated in the previous subquestion, and provide a 95% confifidence interval using asymptotic normality of the maximum likelihood estimator, and the delta method. Enter your estimate for VaR0:99 in the Google form on nestor (you need to login with your University of Groningen account).
(d) Estimate the expected shortfall corresponding to the 99% Value-atRisk, using the results of the previous two subquestions. 数值方法代写
Note: as the data are given as daily returns (and not in Euro’s), the answers to the last two subquestions are expected to be in terms of daily returns as well.
- (10 points) Let f .x1; x2/ D .x1 C x2/2 . Show that the numerical approximation to the Hessian as discussed in week 3 is exact.
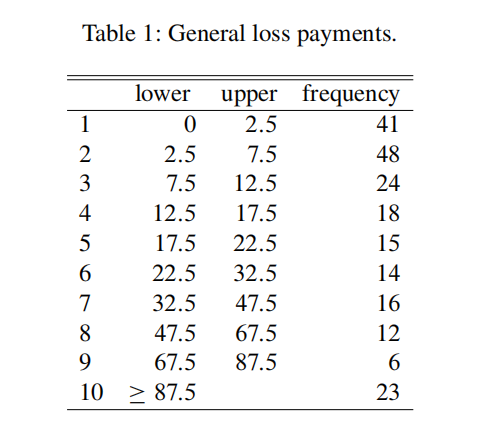
- (10+15 points) In practice, sometimes data are presented in the form of a table with (relative) frequencies. For example a table with individual payments on a general loss insurance is presented in table 1. Assume that the individual data underlying the frequencies in table 1 follow a translated Gamma distribution (Y follows a translated Gamma distribution if we have Y D c C X, with X .˛; ˇ/, and c an additional parameter to be estimated).
(a) Use the information in the table to fifit a translated Gamma distribution by optimizing a loglikelihood function.
(b) Estimate the probability an arbitrary payment exceeds 150, and provide a 95% confifidence interval for that estimated probability. State precisely any assumptions you make.