Intro Math Modeling – MATH-UA 251
数学建模代写 Use the tools and material covered in class, recitation sections, and homework assignments, along with other resources such as textbooks…
Use the tools and material covered in class, recitation sections, and homework assignments, along with other resources such as textbooks and scientifific articles, to perform a research study on the dynamics of pendulums.
(i) Start with a simple pendulum consisting of a spherical mass m anchored to a fifixed point O via a mass-less rod of length ` (cf. Fig. 1(a)). Perform a dimensional analysis on the problem to fifind the period of oscillation τ (i.e., time scale of the system). Use the Newton’s second law to write the governing ordinary difffferential equation (ODE); a solution to this nonlinear equation should relate θ, or an equivalent variable, to time t. Then, for small deviation angles θ, use linear approximation to linearize the ODE. Analytically solve this linear ODE to fifind θ as a function of t. Let θ = θ0 and θ˙ = 0 be the initial conditions of the problem. Using the concept of dimensional homogeneity, fifind the time scale of the problem from the obtained solution. Compare it to the one you found from dimensional analysis. 数学建模代写
(ii) Use the Euler method to numerically solve the original nonlinear ODE. First, make a plot of θ versus the dimensionless time, t/τ , for difffferent time steps ∆t. This plot should cover, at least, a couple of the oscillation periods. Discuss what happens qualitatively as the ∆t changes. Then, for a reasonably small ∆t ( τ ), plot θ versus time for difffferent values of θ0, along with the corresponding analytical solutions to the linear problem. Discuss what happens as θ0 decreases.
(iii) Revisit the problem accounting for the drag force on the mass. Additionally, make plots of θ˙ versus θ for difffferent conditions. Discuss the important characteristics of the plots for system with and without drag. Interpret the results.
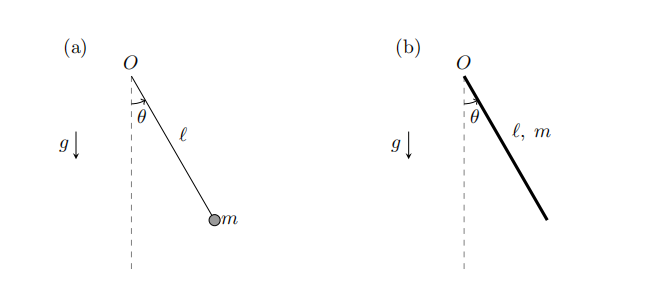
Figure 1. (a) A simple pendulum of mass m, attached to an anchor O via a mass-less rod with length ` . (b) A circular rod of radius a (thickness 2a), mass m, and length ` , connected to an anchor O.
(iv) Revisit the problem when the rod itself has a mass m with no mass connected to it (cf. Fig. 1(b)). When accounting for the drag force, assume that FD is linearly proportional to the magnitude of the normal velocity and the projected area.
(v) Perform an analysis of the double-pendulum system (bonus).
Project write-up 数学建模代写
Write your report as a short technical paper that will describe the problem and background, rationalize your modeling choices, set up the equations, explain all parameters in the model, present the analysis and solutions of the model, and interpret the results. Feel free to analyze the problem beyond what suggested above.
Structure the document as a scientifific report with multiple sections: abstract, introduction, model description, results, conclusions, references. You may write the report using LATEX, Microsoft Word, etc. Regardless, a PDF should be submitted. Long derivations (if any) should be provided in an Appendix. Submit your codes (fully commented) as well, and if needed, provide a user guide for the code either in an Appendix or as comments in the code. References should be provided. Follow the citation style of Physical Review Letters.
The grading criteria include the scientifific content of the report, along with various editorial factors such as organization of the paper, consistency (in notation, units, etc.), readability, and correct/accurate/clear fifigures. In particular, all fifigures should have axis labels (with units, if any), tick labels, legends (if applicable), a self-contained caption (below the fifigure).
The submitted report should present an original work performed by the author. Simple pendulum is a well-known, much studied, problem in Physics. You can, of course, study those prior work, but submit your unique version of the modeling, solution, coding, analysis, interpretation, etc. Please refer to the syllabus for more info on the honor code.



