Intro to Math Methods
Homework #2
数学方法代写 In this homework you will do basic celestial mechanics. Consider a system of ODEs which models the motion of N planets around a star.
-
[100 points] Orbits of Planets in a Solar System 数学方法代写
In this homework you will do basic celestial mechanics. Consider a system of ODEs which models the motion of N planets around a star. The masses of the planets will be denoted with mi and their positions with ri(t), i = 1, …, N. We will assume that the mass of the star m0 is much larger than the masses of the planets (note that for simplicity we set the planet masses to unity), so we can assume that the star remains fifixed at the origin, r0 = 0. Here you can assume that all of the planetary orbits are co-planar, ri = [xi(t), yi(t)] ∈ R2 , although it is strongly recommended that you write your code so that the number of dimensions (2 or 3) can be an input parameter.That way your code can be used to study the impact of a comet coming out of the plane of the solar system without any changes.
Newton’s laws of motion for the planets take the form of a system of second order difffferential equations,
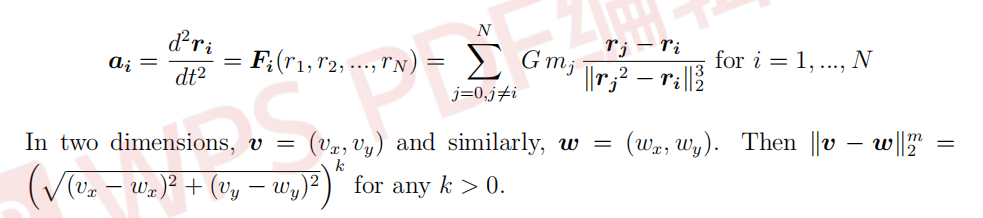
For simplicity, set the gravitational constant G = 1, although good programming practice suggests that you should keep it is a (perhaps global) variable in the code instead of hard-wiring the unit value. You might fifind the notes on MATLAB’s array structure and vectorized operations (refer to vect.m under week 1 lectures).
You will both write your own solvers and use MATLAB’s ode suite. Your task is to fifind the trajectories of the planets in the solar system (i.e., solve for ri(t)). For writing your own solvers, put effffort into writing a code that can integrate any fifirst-order system of ODEs (like forward Euler) and not just the specifific ODEs for gravitational systems The steps below will walk you through the steps to fifind the planetary trajectories.
1.1 [80 points] Single Planet 数学方法代写
Consider now the case N = 1, and denote the position of the single planet with r(t) with length k rk 2 = r. It is well known since Kepler’s time that the orbit of a planet around a massive star is an ellipse with the star being one its foci. The energy of the single planet and star system is the sum of gravitational (potential) and kinetic energies:
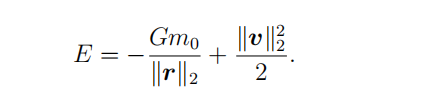 (1)
(1)
Assume that the initial position of the planet is r(0) = [r(0), 0] and set the initial velocity v = dr/dt = [0, v(0)], which ensures that the initial position is either the furthest or the closest to the star on the orbit (i.e., it is a vertex of the ellipse). Try v(0) = 0, 1, 1/2. The system of difffferential equations describing the trajectory of a single planet are given by
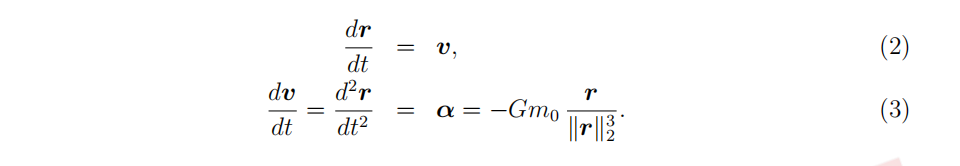
(a) [50 points] Circular Orbit
It can be hard to know if your code is working or not. Let us check for an easier problem – 1oneplanet in a circular orbit. In a circular orbit,
r = [cost,sin t], (4)
with the initial speed v(0) = r(0). Use the MATLAB solver ode45 method to fifind the trajectory and the energy of the planet for a few hundred time steps using a fifixed time step size ∆t = T/NT where NT is the number of time steps. Then compute again the orbit with time step ∆t/2 and again with ∆t/4. Confifirm that the ode45 is fourth-order accurate by comparing the error (obtained position – actual position):
ek = ||Rk − r(k∆t)||2
where Rk is the numerical approximation and r(t) is the actual solution as a function of time t = k∆t. Comment on your observations. Find the largest possible time step size ∆t that ensures that the maximum error in the x and y position of the planet is no larger than 10−2 , i.e., one percent relative error or two digits of accuracy (fifirst solution).
(b) [60 points] Elliptical Orbit 数学方法代写
Using the time step identifified above solve for the trajectory and the energy of the planet for a few hundred iterations using:
- your own routine for (forward) Euler’s method;
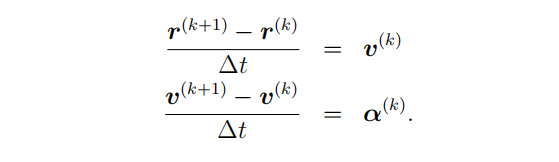
- your own routine for Verlet’s method; and
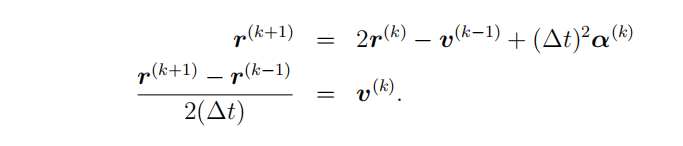
- MATLAB’s adaptive Runge-Kutta method (ode45).
In each of these schemes for all of the difffferent initial conditions describe what you observe and plot the trajectory and the energy over time. Which method would you use and why?
Hint: For plotting you might fifind the MATLAB function polar instead of plot.
You can look at the documentation for an example or type help polar.
1.2 [20 points] Multiple planets & Movies 数学方法代写
This part is for you to play and have fun but also learn how to make scientifific animations (movies). Consider the case N > 1, say N = 5, called the N-body problem. Play around with your adaptive integrator and see if you can construct an example where something interesting happens, and report what you came up with. Make a movie showing of your example. If you can produce a standalone movie fifile (say AVI or MPEG) that would be great – submit that movie with your homework. If not, at least submit a script that can produce the movie in real time.
-
[20 points] Yet Another Approximation of the First Derivative
Using Taylor series, derive the three-point forward difffference formula to approximate the fifirst derivative at x using function valyes at x, x + h, and x + 2h. Obtain an expression for the local truncation error as a function of the step size.



