Midterm Assessment
AMATH 250 Online
数学Midterm代考 You may use any of the content posted on the AMATH 250 Learn site and your recommended course note, but you are NOT…
You may use any of the content posted on the AMATH 250 Learn site and your recommended course note, but you are NOT allowed to get help from anyone, and you are NOT expected to search for answers on the internet. This is intended for you to complete by yourself.
The University of Waterloo subscribes to the strictest interpretation of academic integrity. Faculty members and students bear joint responsibility in assuring that cheating on assignments or any examinations is not tolerated. Students who engage in academic dishonesty will be subject to disciplinary action under Policy 71 (available for your review upon request).
This examination is protected by copyright. Reproduction or dissemination of this document or the contents or format of this document in any manner whatsoever (eg. Sharing the content with other students), without express permission of the instructor, is strictly prohibited.
I confifirm that I will keep the content of this examination confifidential. 数学Midterm代考
I confifirm that I have not received any unauthorized assistance in preparing for or writing this examination.
Student Name and ID (please print) ——————————
Student Signature ——————————
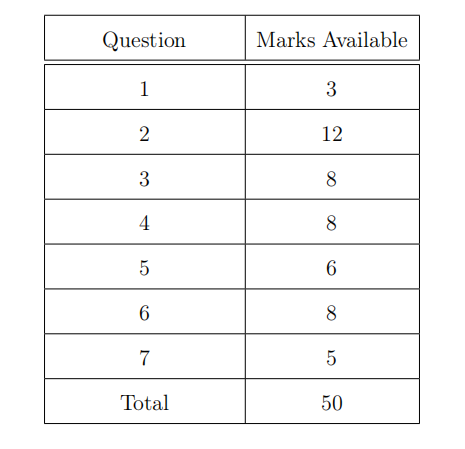
1.50 Recognize the linear and nonlinear difffferential equations. Justify your answers.
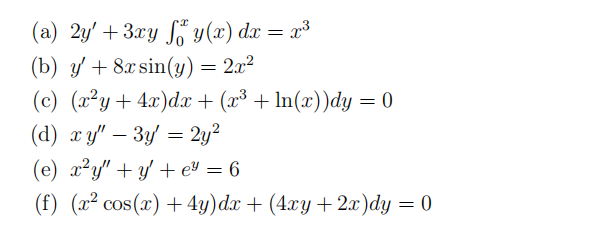
- Find the general solutions (implicit or explicit) to the following equations. 数学Midterm代考

- An object of mass m is dropped vertically from a height h0 about ground level with zero initial velocity. We are interested in its time flflight tf before hitting the ground. Suppose that we do not know any laws of physics but suspect that tf depends on m, h0, the acceleration due to gravity g, and the shape of the object characterized by a dimensionless number s. Use dimensional analysis to determine how tf depends on those other parameters. (The effffect of air drag is assumed to be incorporated into s.)
- Give a qualitative sketch of the solutions of
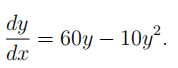
Hint: You do not need to solve the DE. First determine the intervals of increase/decrease and intervals of concavity, then sketch the qualitative shape of
the solutions.
- (a) For the following IVP, predict the behaviour using the Existence/Uniqueness Theorem.
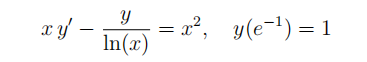
(b) Solve the IVP from part (a). Your fifinal answer may include a defifinite integral.
- Consider the initial value problem
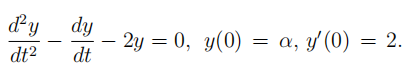 For what value of α, the general solution y(t) approaches zero when t → ∞.
For what value of α, the general solution y(t) approaches zero when t → ∞.



