Final Exam
OMIS 6230
数据分析代考 Petit Gˆateau is an upscale specialty cupcake franchise with sixteen locations across the GTA. Each night, cupcakes are baked at a…
Question 1 [7 points]
Petit Gˆateau is an upscale specialty cupcake franchise with sixteen locations across the GTA. Each night, cupcakes are baked at a central facility and delivered to franchises prior to their opening. Cupcakes are sold individually at each franchise location for $3.49. Franchises are charged a cost of $0.89 for each cupcake that is provided to them by the central facility. Cupcakes that are not sold at the end of the day are discarded; the central facility credits the stores $0.25 for each unsold cupcake even though it costs them $0.54 to construct and bake. Since the start of the pandemic, Petit Gˆateau’s head offiffiffice has observed signifificant demand volatility. As a result, they want to be more data-driven when making operational decisions. To do this, they have compiled a data set of the most popular SKU over the last 135 days by combining the sales from all of its 16 stores (see Dataset.xlsx ).
For prices, round to two decimal places. For order sizes, round to the nearest integer.
(a) What is the mean and standard deviation of demand for the most popular SKU using the data set that has been collected?
(b) Comment on why the Newsvendor model is appropriate to study Petit Gˆateau’s inventory practices as compared to the EOQ and periodic-review inventory models?
(c) What are the Newsvendor parameters p, w, c and v? 数据分析代考
(d) Using the single-period Newsvendor, what is the optimal base-stock level for the most popular SKU from the perspective of the central facility assuming the demand distribution is not known?
(e) Using the single-period Newsvendor, what is the optimal base-stock level for the most popular SKU from the perspective of the central facility assuming demand is normally distributed?
(f) Given the information provided in the question, are the single-period ordering policies that are derived in questions (d) and (e) optimal for the multi-period setting?
(g) What is the optimal wholesale price (denoted by w∗ ) if a franchise shares 15% of its profifits with the central facility?
(h) What is the optimal buy-back price (denoted by b∗ ) that maximizes the expected profifit of the supply chain?
(i) From the perspective of a single franchise, what is the optimal order quantity for the most popular SKU using the price-only (use w and b), revenue-sharing (use w∗ and b), and buy-back (use w and b∗ ) contracts? Please assume that all franchises have identical values for the mean and standard deviation of demand which you should assume is normally distributed.
(j) Suppose that a franchise wants to start selling a 2-pack of cupcakes and wishes to achieve a 90% service level, i.e., the critical fractile is 0.90. Using the original problem parameters p, w, c, and v, what would the per pack selling price be? Comment on whether this price is realistic.
Question 2 [5 points] 数据分析代考
In order to make cupcakes at the central facility, four primary ingredients are used: cupcake mix, eggs, butter, and oil. The average annual demand for eggs is 98,000 cartons, the average weekly demand for cupcake mix is 5 pallets, and the average monthly demand for butter and oil is 4000 and 3000 pounds, respectively. Each pallet of cupcake mix weighs exactly 255 pounds and each carton of eggs weighs exactly 2.19 pounds. The table below presents the difffferent costs per unit for each ingredient.

Since all products are ordered from the same supplier, it is possible to design an EOQ policy that has the supplier ship all of the products on the same truck. However, notice that some of the ingredients need to be refrigerated when transported. As a result, a special mixed-use truck that transports both regular and refrigerated items must be used when the ingredients are shipped together. The mixed-use truck has a 15,000-pound weight limit and can transport no more than 8 pallets of cake mix. Further, the ratio of butter divided by oil in the mixed-use trucks must be greater than 122%. The delivery fee associated with coordinated shipments is $99. Trucks dedicated to transporting a single item have a 25,000-pound weight limit and there is a $64 delivery fee. Finally, note that while whole pallets must be shipped on each truckload, one can assume that egg cartons are infifinitely divisible.
(a) Why is the EOQ model appropriate to study the central facility’s inventory practices?
(b) How many decision variables are in this nonlinear optimization model?
(c) What is the smallest number of constraints that must be added to the optimization model to ensure that all order frequencies are identical?
(d) Write down the constraint associated with the ratio butter divided by oil. Please make sure this constraint is linear in the decision variables.
(e) What is the sum total cost of ordering the ingredients separately?
(f) Using Analytic Solver, solve the optimization model. You can also use the built-in solver tool by initializing the decision variables. That is, before opening the solver window, type the number 1 in each of the cells corresponding to decision variables. Regardless of the computational approach, what is the optimal cost of ordering all ingredients in a coordinated shipment?
(g) Should Petit Gˆateau order the ingredients in a coordinated shipment or order each ingredient separately? How much is the cost savings given your recommendation?
(h) Where is the cost savings coming from?
Question 3 [5 points] 数据分析代考
Each year, the central facility uses 5500 pounds of sugar to make their cupcakes. Unfortunately, their current supplier has gone out of business and thus, Petit Gˆateau is searching for a new one. They are considering four vendors each with difffferent all-unit price discount structures (see table below).
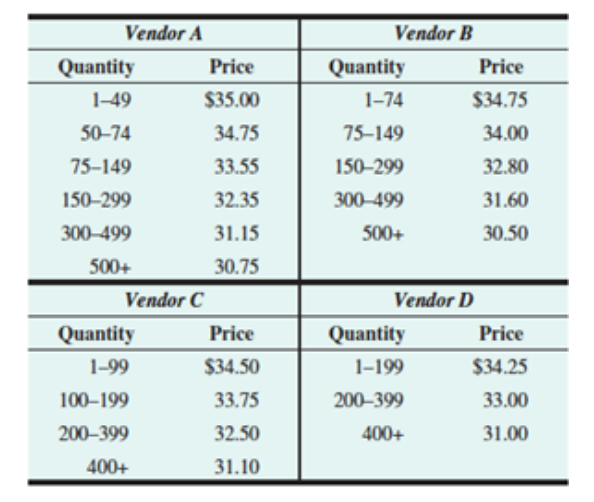
There is no cost of ordering from any of the suppliers and they are all promising a fifive-day lead time. However, it take exactly 2-hours for the warehouse manager at Petit Gˆateau to process each shipment (she is paid $28 per hour). Note that the annual holding cost is $4.44 per pound of sugar and the variability (standard deviation) in the amount of sugar used per day is equal to 33 pounds.
(a) What is the optimal order quantity when ordering between 300-499 pounds from Vendor A and between 200-399 pounds from Vendor D?
(b) What is the optimal order quantity for each of the vendors?
(c) How much safety stock should be maintained to ensure a 95% service level?
(d) By calculating the yearly total inventory costs for each vendor, which should be selected if Petit Gˆateau wants to minimize costs. What is this cost and how many orders are placed per year?
Question 4 [8 points] 数据分析代考
Instead of throwing out day old cupcakes, Petit Gˆateau has started selling them in packs of four and is looking at a dynamic way to price them. The 4-cupcake packs are sold starting at 6pm until the store closes at 12am. At the beginning of each hour, the price of the package changes to dynamically adapt to the expected demand that will be observed over the next hour (see table below). The price of the 4-pack cupcakes should increase hour-after-hour until the highest price is offffered at 8pm. Prices should then decrease thereafter. Suppose that today, at one store, there are 384 day-old cupcakes.
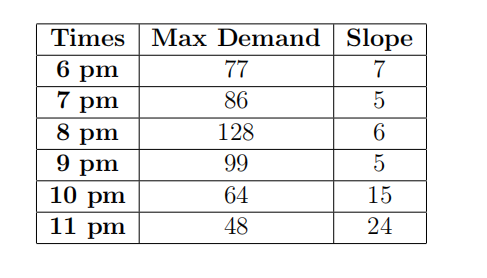
Formulate and solve a nonlinear optimization model to determine the optimal hourly prices for 4-pack cupcakes to maximize total profifit over the 6-hour period. Then, answer the following questions:
(a) What is the break-even price that a Petit Gˆateau franchise can sell a 4-cupcake pack?
(b) What is the objective function associated with the model that determines the optimal expected profifit of selling 4-cupcake packs? How many decision variables are there?
(c) Write down the constraints that ensure demand of 4-cupcake packs does not exceed supply and that prices should exceed the salvage value?
(d) What is today’s optimal expected profifit assuming that a franchise does not consider any of its other products when setting the price of the 4-cupcake pack?
(e) What is the optimal price of a 4-cupcake pack between 8pm and 9pm assuming that a franchise does not consider any of its other products when setting its prices? 数据分析代考
(f) Why is it important to consider the selling price of freshly baked cupcakes when formulating the model to determine an optimal pricing strategy for 4-cupcake packs? What constraint(s) must be added to the formulation to account for this when pricing the 4-cupcake packs?
(g) Including the new constraint(s), what is today’s optimal expected profifit? What is the optimal price of a 4-cupcake pack between 7pm and 8pm?
(h) What type of customer segmentation strategy is Petit Gˆateau employing by selling day-old cupcakes in packages of four? Please explain how it applies in this scenario.
(i) Because each store caters to a difffferent set of customers, the linear price-response functions will diffffer. If each store uses an equivalent optimization model, but difffferent price response functions to set its prices, what type of segmentation strategy is Petit Gˆateau employing?
(j) Do you think that this dynamic approach to selling day-old cupcakes is a good one? Provide one positive comment and one critique about this revenue management strategy.



