CMPUT 366
Midterm Exam
智能系统代写 The midterm exam is closed book. You are not allowed to use any resources or equipment other than this exam, a pen/pencil, and a single-page “cheat sheet”.
Total points: 60
The midterm exam is closed book. You are not allowed to use any resources or equipment other than this exam, a pen/pencil, and a single-page “cheat sheet”.
You are not allowed to use your own scratch paper. Instead, use backsides of the exam pages as scratch paper for your work.
You are not allowed to use any equipment (e.g., phones, computers, tablets, etc.)
You are not allowed to communicate with anybody except the examiners/proctors.
-
(Short Answers) 智能系统代写
(a) [2 points] What are the semantics of a belief network? (Hint: What guarantee does it make about conditional independence?)
(b) [2 points] What is an admissible heuristic?
(c) [2 points] For what kind of problem is local search appropriate?
(d) [2 points] Explain why hill-climbing is incomplete.
(e) [2 points] Explain why variable elimination can be more effiffifficient than just computing the full joint distribution and then normalizing.
(f) [2 points] Why is loss on the training dataset not a good estimate for generalization performance?
(g) [2 points] What is selection bias?
(h) [2 points] Consider a computation with inputs x1, x2, x3 and output y. What is computed by backward-mode automatic difffferentiation for each intermediate value si?
(i) [2 points] Give an expression for the value of a single rectifified linear unit (relu), with inputs x1, x2, weights w1, w2, and offffset (bias) b.
(j) [2 points] Why are convolutional networks more effiffifficient to train than fully-connected feed-forward networks?
-
(Search)
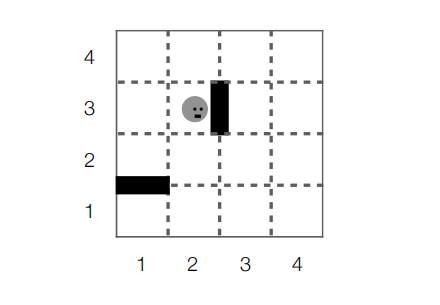
GridBot is an agent that lives in the grid world pictured above. GridBot can move a single square up, down, left, or right, but not diagonally, and not through either of the two walls. GridBot starts in square (x, y) = (2, 3), as pictured. GridBot’s goal is to get to either of the bottom corners (1, 1) or (4, 1) using the smallest number of actions.
(a) [2 points] How many states does this search problem have?
(b) [2 points] Let succ be the successor function for this search problem. What are the return values for the following function calls:
i.succ((2, 3)) =
ii.succ((3, 2)) =
iii. succ((1, 1)) =
iv.succ((4, 1)) =
(c) [2 points] Consider the following heuristic function:
h((x, y)) = y − 1
Is the heuristic function h an admissible heuristic for this problem? Why or why not?
(d) [3 points] Either construct an admissible heuristic function h0 for this problem that dominates h, or else explain why this is impossible.
(e) [4 points] List the paths that are removed from the frontier by A∗ using the heuristic h from the previous question, in the order in which they are removed. You may stop once you remove a path to a goal node.
-
(Uncertainty) 智能系统代写
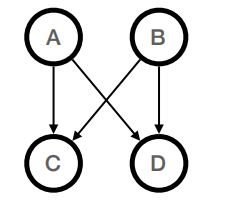
(a) [3 points] What factorization of the joint distribution P(A, B, C, D) does the belief network below represent?
(b) [3 points] Is the belief network below also consistent with the same joint distribution? Why or why not? (Hint: What factoring does the belief network below represent?)
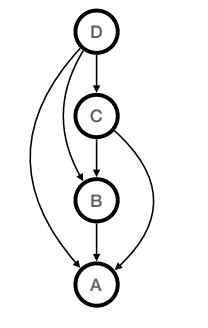
Yes. This belief network represents the factoring P(A | B, C, D)P(B | C, D)P(C | D)P(D),which is a valid factoring for any joint distribution
P(A, B, C, D) by the chain rule.
(c) [3 points] Draw a belief network that represents the factoring
P(A, B, C, D) = P(D | C)P(C | A, B)P(A)P(B).
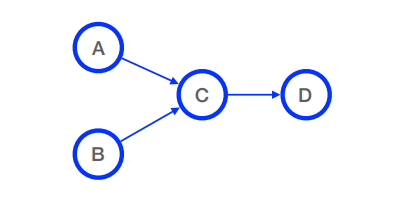
(d) [2 points] List the factors that would be constructed as the fifirst step of variable elimination for the belief network from question (3c).
(e) [3 points] List the new factor, and the operations used to create it, when the variable elimination algorithm eliminates B from the list of factors in question (3d).
(f) [3 points] Draw the graph for the post-intervention distribution for the query
P(Y | do(W = true))
for the following causal model:
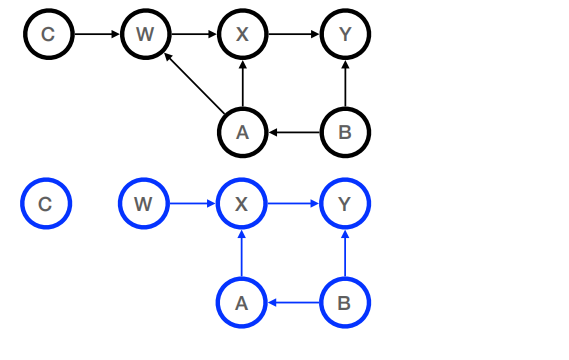
-
(Neural Networks) 智能系统代写
(a) [3 points] What is the output of a convolution operation on the matrix

(b) [3 points] What is the output of a 2 × 2 maximum pooling operation on the matrix
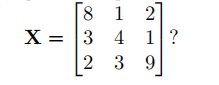
(c) [4 points] Consider the following set of training examples (x, y):
E = {(5, 0000011111),
(4, 00001111),
(3, 000111),
(2, 0011),
(1, 01)}
Assume that the inputs and outputs are represented as a single activation; that is, the input 5 represents the value 5 rather than a one-hot vector; the output 01 is a sequence of the value 0 followed by the value 1.
Can a recurrent neural network that recurs though the outputs only achieve a perfect training loss on E with suffiffifficient training and a suffiffifficiently large hidden layer? Why or why not?



