Lab 4: Non-negative Matrix Factorization
机器学习lab代写 We use the ORL Face database for this assignment, which consists of 400 images for 40 people, each of size 112 x 92. These…
Data
We use the ORL Face database for this assignment, which consists of 400 images for 40 people, each of size 112 x 92. These images were taken at different times, with varying lighting and for different facial expressions. All faces are in an upright position with a frontal view, with a slight left-right rotation. To use this dataset, we perform some pre-processing on them, listed here –
- We use only the train split for this data (the first 9 images per person).
- We construct a data matrix data_train of size 10304 x 360 by flattening all the faces.
- data_train is divided by the max value present in the images to normalize the data and avoid overflow issues, giving us the final data matrix V.
Performing NMF 机器学习lab代写
To perform NMF, we want to decompose the matrix ?=??. To do so, we’ll follow these steps
- Create an NMF function nmf( V, rank, max_iter, lambda) to implement all of these steps.
- Initialize B and W randomly, and make sure W has unit-sum columns (each column should sum to 1).
- Calculate the initial objective. It will be helpful to define a new function for the objective, compute_objective(V, W, B) that returns the objective value.

6.Repeat steps 4 and 5 until the stopping criteria are reached.
7.Stopping Criteria: Stop when the absolute difference of objective values is smaller than or equal to l (or) the max number of iterations has been reached.
Notes:
- Function definitions and descriptions have already been provided in the template files.
- 1WT and BT1 are another way of writing the sum of each column of W and B, respectively.
o What these denominator terms are doing are normalizing the columns of W and B such that they have unit sum. You should ensure that the columns of your W normalize to 1.
Validation on the ORL Faces Dataset 机器学习lab代写
- Plot the new bases from your nmf function. Use rank=40, max_iter=500, and lamda=0.001. Place all 40 iamges in a single figure, each in its own subfigure.
- Compare your results with predefined NMF functions in MATLAB/Python.
Performing NMF with Sparsity Constraints
The process for performing sparse NMF is the same as above, with a few changes to Step 4.
- Create a sparse NMF function nmf_sparse( V, rank, max_iter, lambda, alpha, beta) to implement all of these steps.
- Initialize B and W randomly, and make sure W has unit-sum columns (each column should sum to 1).
- Calculate the initial objective. It will be helpful to define a new function for the sparse NMF objective, compute_objective_sparse(V, W, B, alpha, beta) that returns the objective value.
- Perform the iterations
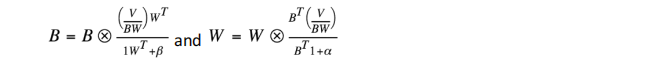
where specifies element-wise multiplication and all divisions are element-wise division.
- Calculate the new objective function value using compute_objective_sparse(V, W, B, alpha, beta).
- Repeat steps 4 and 5 until the stopping criteria are reached.
- Stopping Criteria: Stop when the absolute difference of objective values is smaller than or equal to l (or) the max number of iterations has been reached.
Notes:
- Function definitions and descriptions have already been provided in the template files.
- You should ensure that you perform the normalization by 1WT+α and BT1+β
Validation on the ORL Faces Dataset 机器学习lab代写
- Plot the new bases from your nmf_sparse function. Use rank=40, max_iter=500, lambda=0.001, alpha=100, and beta=1. Place all 40 iamges in a single figure, each in its own subfigure.
Deliverables:
If you use Python, use the provided Jupyter Notebook template for all problems, which is also available at following link:
https://colab.research.google.com/drive/1n3QW690QA4jGiT5vmpg2uY2ddDIFTPcb?usp=sharing
MATLAB: A completed lab_4.m or lab_4.mlx source file with corresponding nmf.m, ssnmf.m, compute_objective.m, and compute_objective_ss.m files containing function definitions.
Python: Lab4_FirstnameLastname_JHID.ipynb with appropriate function definitions for nmf, nmf_sparse, compute_objective, and compute_objective_sparse



