Module Title: Discrete Time Finance
Assessed Assignment
离散时间金融代写 Consider a binomial market model with one stock and one bank account. Trading takes place in discrete time and one period’s length…
Consider a binomial market model with one stock and one bank account. Trading takes place in discrete time and one period’s length is 1 month. The stock has an initial price of S0- Each month, the stock price can go up by a factor u with probability pu or down by a factor d = 1/u with probability pd = 1 pu. The monthly risk-free interest rate is r (per month). In the above market, consider the down and out barrier Put option defined by the following payoff:
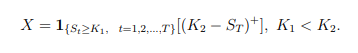
-
Estimate numerically, using Monte Carlo simulations of 1000 price paths, the expected discounted pay off of the above option. For your simulations use the following parameter values: 离散时间金融代写

and take two different values for the maturity time T = 3 and T = 10. Do the simulation of 1000 price paths in each case 10 times and determine the mean and standard deviation of the obtained expected discounted payoffs. Interpret your findings.

- Repeat the procedure above using the risk neutral probability measure instead of thephysical measure. Estimate the expected discounted payoff for the two different maturity times given in the previous subquestion. 离散时间金融代写
- Calculatethe risk neutral expected discounted payoff for T = 3 manually.
- How many different values can the payoff take for T = 40?Present your calculations and arguments.
- Modify your program in such a way that you can change the value of u. Use all otherconstant parameters as in 1. and T = 6. Simulate the expected discounted payoff under the risk-neutral measure for values of 1.2 u 1.1 such that you cover the given interval with small Plot the graph of the expected discounted payoff as a function of u. Discuss your result.
- Consider now the American version of the above option, that is when the owner of the option is allowed to exercise it at time 0 < t ≤ T . The corresponding payoff will be 离散时间金融代写
![]()
Compute manually the price of the option with T = 3. Explain the procedure you used. 离散时间金融代写
There is no word count for this assignment. The report should typed as one whole document (no hand-written parts will be accepted). Code should be included in the appendix and not in the main report. One hard copy of the assignment must be submitted to G. Aivaliotis’s letterbox on level 8 School of Mathematics building and an electronic copy must be uploaded on Minerva by Tuesday 3/12/2019, 12 noon. Failure to meet this initial deadline will result in a reduction of marks. Assignments submitted later than Friday 6/12/19, 12 noon, will receive a mark of 0. Faxed or emailed copies of the report will not be accepted. A signed statement on plagiarism has to be enclosed with your hard copy.



