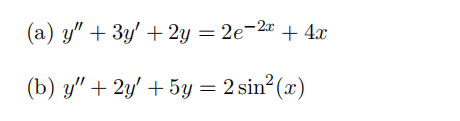AMATH 250 Online Assignment 6
线性函数代写 Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.You…
Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.You may use the course materials posted on the course website and the optional text as references. You are also allowed to discuss ideas with your classmates, the course instructor and TAs. Please do not post fifinal answers or give away too much on Piazza; it will be monitored closely. Your submitted work must be written upon your own and should indicate your knowledge of the material.
Academic Integrity Declaration (AID): Fill out the Academic Integrity Declaration form and upload as a page 1 to Crowdmark. 线性函数代写
I declare the following statements to be true:
- The work I submit here is entirely my own
- I have not used any unauthorized aids
- I am aware that misconduct related to examinations can result in signifificant penalties including failing the course and suspension, as outlined in Policy 71
- I have discussed the assignment with the following people (if any):
- Write your name and the date in the box below, then upload this page to Crowdmark.
Each question should be uploaded separately to Crowdmark. 线性函数代写
- Consider the functions y1(t) = sin(t²) and y2(t) = cos(t²).
(a) Use the defifinition to show that the functions are linearly independent on (−1, 1).
(b) Show that the Wronskian of y1 and y2, W(y1, y2), is zero at t = 0.
(c) Explain why the results of (a) and (b) do not contradict Lemma 2 in Section 4.2 of the online notes.
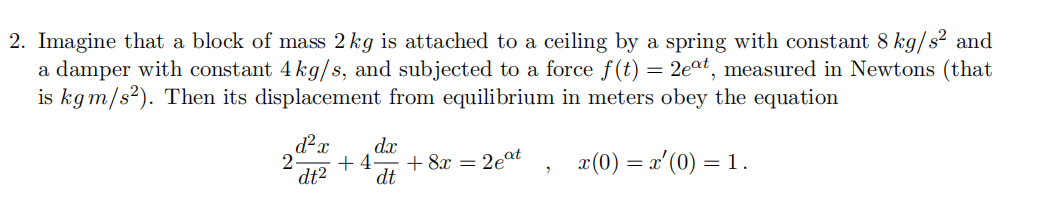
Solve the DE for the following values of ↵. (It is strongly recommended that you solve for the general solution and IC-determined constants fifirst, in terms of ↵. Then plug in to get the specifific solution for each case.). Describe what happens to the motion of the block in the long run for each case. Do these results seem realistic, or is there a problem with our mathematical model?
(a) α= −1
(b) α= 0
(c) α= 1
- Find the general solution to the given equations: 线性函数代写