MAT301H5S
Groups and Symmetries
组和对称代写 The University of Toronto Mississauga and you, as a student, share a commitment to academic integrity. You are reminded that…
The University of Toronto Mississauga and you, as a student, share a commitment to academic integrity. You are reminded that you may be charged with an academic offence for possessing any unauthorized aids during the writing of an exam. Clear, sealable, plastic bags have been provided for all electronic devices with storage, including but not limited to: cell phones, smart watches, SMART devices, tablets, laptops, and calculators. Please turn off all devices, seal them in the bag provided, and place the bag under your desk for the duration of the examination. You will not be able to touch the bag or its contents until the exam is over. 组和对称代写
If, during an exam, any of these items are found on your person or in the area of your desk other than in the clear, sealable, plastic bag, you may be charged with an academic offence. A typical penalty for an academic offence may cause you to fail the course.
Please note, once this exam has begun, you CANNOT re-write it. 组和对称代写
Instructions: 组和对称代写
- This exam consists of 8 questions for a total of 80 marks.
- The exam consists of 9 pages including the cover page. Unless otherwise stated, show your work.
- If you need more space, use the back of a page; clearly indicate when you have done this. 组和对称代写
| Question | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | Total |
| Points | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 80 |
| Score |
NOTE: Unless otherwise stated, the operation in Z and Q is ordinary addition, the operation in Zn is addition modulo n, the operation in U (n) is multiplication modulo n, the operation in GL(2, R) is matrix multiplication, and the operation in Sn and Dn is composition. 组和对称代写
Question 1. Parts (a) and (b) are unrelated. 组和对称代写
(a) (5 Marks) Suppose G is a group with 7 elements of order Prove that G is not cyclic.
(b) (5 Marks) Suppose x ∈ G, where G is a If a, b ∈ Z such that b|a, prove that ⟨xa⟩ ⊆ ⟨xb⟩. 组和对称代写
Question 2. Parts (a) and (b) are unrelated.
(a) (5 Marks) Show that Q+ (the set of positive rational numbers) under multiplication is not isomorphic to Q under addition. 组和对称代写

(b) (5 Marks) Is S4 isomorphic to Z6 ⊕ U (5)? If yes, prove If no, justify your answer.
Question 3. (10 Marks) Let G = Z Z10, and let H = g G : g = or g = 1 . Is H a subgroup of G? If yes, prove it, if no, give an example showing one of the properties of a subgroup fails. 组和对称代写
Question 4. (10 Marks) Let G be an Abelian group, and let G6 = {g ∈ G : g6 = e}, and
G6 = {g6 : g ∈ G}. Prove that G/G6 ∼= G6. 组和对称代写
Question 5. Let 组和对称代写
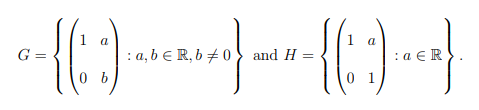
(a) (3 Marks) Prove that G is a group under usual matrix multiplication. 组和对称代写
(b) (3 Marks) Prove that H is a subgroup of G.
(c) (4 Marks) Is H a normal subgroup of G? Justify your answer. 组和对称代写
Question 6. (10 Marks) Suppose φ : Z30 G is a surjective homomorphism, where G = 5. Find ker φ. 组和对称代写
Question 7. (10 Marks) Prove that Aut(S10) is not cyclic. 组和对称代写
Question 8. (10 Marks) A subgroup H of a group K is called a characteristic subgroup if φ(H) = H for all φ Aut(K). Prove that if H is a characteristic subgroup of K, and K is a normal subgroup of G, then H is a normal subgroup of G. 组和对称代写
In submitting this test, I confirm that my conduct during this test adheres to the Code of Behaviour on Academic Matters. I confirm that I did NOT act in such a way that would constitute cheating, misrepresentation, or unfairness, including but not limited to, using unauthorized aids and assistance, impersonating another person, and commit- ting plagiarism. 组和对称代写
Please sign your name, to confirm the above. 组和对称代写



