BEEM103
Optimization Techniques for Economists
Exam
经济学家的优化技术代考 Full work must be shown in the answer document you upload and the reasoning underlying a conclusion must be made clear. Please write legibly.
Duration: 2 hours + 30 minutes upload time
No word count specified.
Answer ALL questions.
Full work must be shown in the answer document you upload and the reasoning underlying a conclusion must be made clear. Please write legibly.
This is an OPEN book paper.
Additional materials needed:
None
1. (10 points) Determine the first derivative of the function 经济学家的优化技术代考
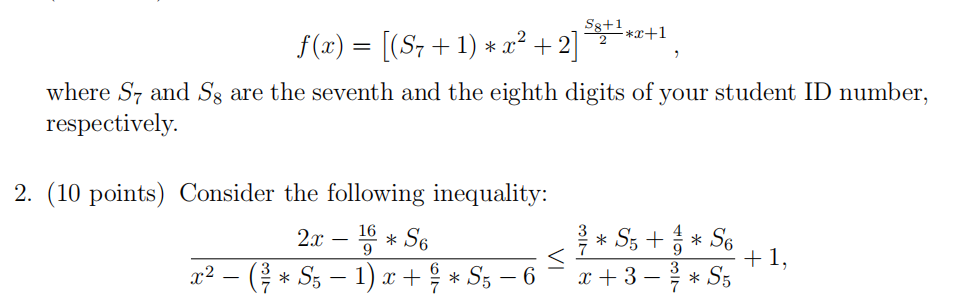
where S5 and S6 are the fifth and sixth digits of your student ID number, respectively. Find the values of x that satisfy the above inequality.
- (15 points) Your line manager has received a report from the market analyst team that the demand function for the company’s product is given by
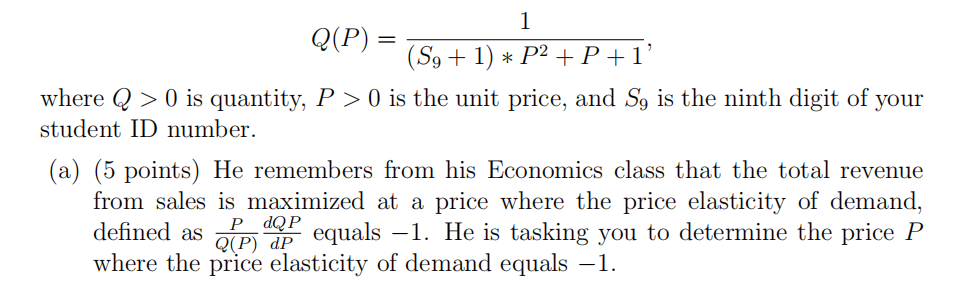
(b) (10 points) You want to be very thorough and make sure this is indeed the total revenue maximizing price level. Determine the price level that maximizes the total revenue function. Is the second-order condition for a maximum satisfied at the optimal solution (i.e. locally)?
-
(15 points) Find and classify the critical points of the function 经济学家的优化技术代考
f(x, y) = x 2 y − 2xy2 + 3xy + 4
- (15 points) A firm produces two goods, A and B, and their production uses the same resource. The company has already purchased b tons of this resource that cannot be returned. Hence, it must be all used up during production. The firm needs to allocate the resource between the production of its products to maximize its total revenue. The revenue generated by the two products (in millions of pounds) are given by
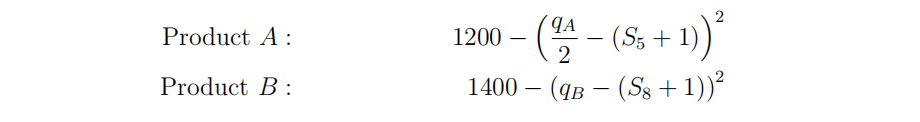
where qA and qB denote the amount of the resource used in the production of product A and B, respectively, and S5 and S8 are the fourth and fifth digits of your student ID number, respectively.
(a) (6 points) Use the method of Lagrange multipliers to determine the optimal allocation of the resource between the production of the two products that maximize the firm’s total revenue.
(b) (9 points) Let b = 17 and assume that the firm is offered one additional ton of the resource for the price of 0.2 million pounds. Should the firm purchase the extra ton of the resource?
-
(20 points) A government agency has made a fund available to firms to finance training projects for their employees. Two firms have submitted their applications. Firm A estimates that their project will generate 经济学家的优化技术代考
T R1(x) = 100, 000 + 8, 000 ∗ x − 0.1 ∗ x 2
revenue for the firm, where x ≥ 0 denotes the funding received by the firm. Firm B estimates that their project will generate
T R2(y) = 150, 000 + 4, 200 ∗ (S9 − 0.5) ∗ y − 0.2 ∗ y 2
revenue for the firm, where S9 is the ninth digit of your student ID number, and y ≥ 0 denotes the funding received by the firm.
The head of the government agency has decided that at most ↔58,000 will be allocated between the two firms. He would like to allocate the fund to maximize the overall revenue generated by the two projects. Use the Kuhn-Tucker method to determine the optimal allocation of the fund taking into account all three constraints.
-
(15 points) Consider a household that maximizes its lifetime utility
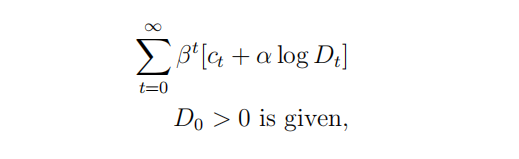
where ct is consumption of nondurable goods and services, Dt is consumption of durable goods, and β ∈ (0, 1) and α > 0 are real parameters.
While nondurable goods and services are consumed immediately, durable goods are not consumed in one use. Instead they depreciate over time with the depreciation rate δ ∈ (0, 1). Moreover, durable goods must be “ordered” in advance, meaning that the quantity of durable goods Dt is taken as given by the household in period t. Therefore, the household chooses its durable goods for period t + 1 (Dt+1) in period t. Consequently, the households budget constraint is given by:
ct + pDt+1 = yt + (1 − δ)Dt
where p > 0 is the relative price of durables in terms of nondurables and yt > 0 is an exogenous income process the household takes as given.
(a) (6 points) Set up the Lagrangian and derive the first-order conditions of the problem.
(b) (9 points) Combine the first-order conditions and derive an expression for Dt and ct only as a function of the parameters of the model and the income process yt .



