CS4186 Computer Vision and Image Processing
计算机视觉代写 This paper has 9 pages (including this cover page). This paper consists of 15 questions.
This paper has 9 pages (including this cover page).
1. This paper consists of 15 questions.
2. Answer ALL questions.
1. This is an open-book examination.
Answer ALL the questions below.
Section A (short questions) 计算机视觉代写
Five marks (5%) for each question
Q1: Which of the following is not correct? Please briefly explain the reason why this statement is not correct.
a) RANSAC does not introduce randomness in model estimation;
b) SIFT is robust to rotations;
c) Pixels at the junction of horizontal and vertical lines could be the corner.
Q2: Please brief explain the reason why the image should be smoothed before detecting the edge in Sobel edge detection.
Q3: Given two Gray images with different image content, when we build the image histogram for each image, whether there is the chance that the two histograms could be the same? Please briefly explain the reason.
Q4: In image matching, please compare the matching speed of the following two methods and briefly explain the reason. 1) Bag of Words; 2) SIFT only.
Q5: Please show one application of structure from motion, and explain the reason that structure from motion could bring benefits to the application.
Q6: Please explain how SIFT feature achieves scale invariance. 计算机视觉代写
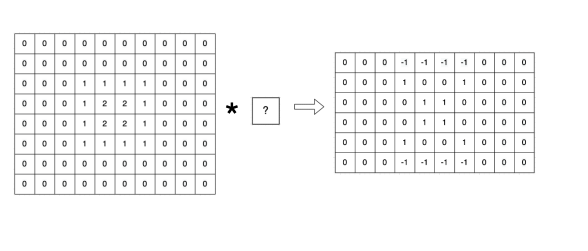
Q7: Please provide one mystery convolution operator, such that convolving the left below (*) with this operator leads to the result on the right. You don’t need to provide the calculation process.
Q8: Please briefly compare the Gaussian filter and box filter when blurring the image. The box filter is an average-of-surrounding-pixel based filter.
Q9: In an image, three pixels, (?, ?) = (0, 0), (1, 0), (0, 1), correspond under the affine transformation to (?′, ?′) = (0, 0), (1, 0), (1, 1). Please find the affine transformation. You don’t need to provide the calculation process.
Q10: Please explain the reason that we need to derive the epipolar lines for stereo matching.
Section B (long questions)
Q11: A pinhole camera has focal length 10mm. Each pixel is 0.1mm×0.1mm and the image principle point is at pixel (200,200). Pixel coordinate starts at (0,0) in the upperleft corner of the image.
1) Show the 3×3 camera matrix for this camera. (3 marks)
2) Given a 3D scene point in world coordinate P = (0, 2, 4). Moreover, the rotation matrix R and translation matrix T (extrinsic parameters) are given as follows,

Please calculate the projection matrix that projects the P onto the image plane, and calculate the 2D image coordinate that corresponds to P. (4 marks)
3) The point P is on a ray with the direction (in world coordinate) ?=(1, 0, 0). Please describe the formula of 2D line based on the perspective projection of this ray in 3D space on the 2D image plane. (5 marks)
Q12: 1) Can the Lucas-Kanade method provide the reliable estimation on the optical flow when the motion is along edges? You can give one example for illustration. (4 marks) 计算机视觉代写
2) Given two images I1 and I2, as well as the optical flows u(x, y) and v(x, y) denoting the motions in horizontal and vertical directions, we have I1(x+u(x,y), y+v(x,y))=I2(x, y). Please describe how to perform forward warping from image I1 to image I2. Will the forward warping result in image holes and how to resolve this issue? (4 marks)
3) Optical flows u(x, y) and v(x, y) denote the motions in horizontal and vertical directions. The affine motion is given by:
u(x,y)= b1+ b2x+b3y
v(x,y)= b4+ b5x+b6y
Under the brightness constancy equation, what is the minimal number of pixels required to estimate the optical flow? Please explain the reason for your answer. (4 marks)
Q13: 1) A SIFT descriptor represented by a vector of 128 numbers can be regarded as being grouped in 16 consecutive groups of 8 numbers each. What does each group of 8 numbers represent? (3 marks)
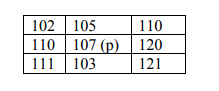
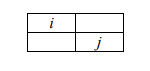
2) Compute the local binary pattern for the central pixel p given the pixel value and 3×3 neighbouring pixel values. In particular, please create the 8-bit number b1b2b3b4b5b6b7b8, where bi = 0 if neighbouring i has value less than or equal to p’s value and 1 otherwise. The upper left has the index 1, and the order is in clock-wise. (3 marks)
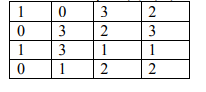
3) Compute the co-occurrence matrix of the following gray-tone image (the pixel values are in
the range of [0, 3]), with the spatial relationship d=(1, 1). (4 marks)
The illustration of d=(1,1) for two pixels i and j is shown in the following figure:
Q14: Affine transformation:
1) Provide the proof that parallel lines are still parallel after affine transformation. (4 marks)
2) Provide the proof that the combination of rotation (2D in-plane) and scale is still the affine transformation. (4 marks)
Q15: The following figure shows a stereo camera set up with two pinhole cameras O1 and O2. The 3D scene point P is projected to p by the first camera O1. 1) Complete the figure below by drawing and indicating a) baseline; b) epipoles; c) epipolar line (for p) in the image plane formed by O2. (4 marks)
2) Please provide the reason that why all epipolar lines intersect at the epipole. (4 marks)



