Exam 1
CS525 – Midterm Exam
计算机mid代考 The exam is 90 minutes long Multiple choice questions are graded in the following way: You get points for correct answers…
Instructions
- Things that you are not allowed to use
– Personal notes
– Textbook
– Printed lecture notes
– Phone
- The exam is 90 minutes long
- Multiple choice questions are graded in the following way: You get points for correct answers and points subtracted for wrong answers. The minimum points for each questions is 0. For example, assume there is a multiple choice question with 6 answers – each may be correct or incorrect – and each answer gives 1 point. If you answer 3 questions correct and 3 incorrect you get 0 points. If you answer 4 questions correct and 2 incorrect you get 2 points. . . .
- For your convenience the number of points for each part and questions are shown in parenthesis.
- There are 5 parts in this exam
- SQL (32)
- Relational Algebra (26)
- Index Structures (24)
- I/O Estimation (18)
Part 1 SQL (Total: 32 Points) 计算机mid代考
Consider the following database schema and instance:

Hints:
- When writing queries do only take the schema into account and not the example data given here. That is your queries should return correct results for all potential instances of this schema.
- Attributes with black background form the primary key of an relation. For example, lName is the primary key of relation location.
- The attribute crimeId of relation account is a foreign key to the attribute id of relation crime.
Question 1.1 (6 Points)
Write an SQL query that returns the names of suspects for murders on locations owned by the Queen. Make sure that your query returns each such person only once.
Question 1.2 (8 Points)
Write an SQL query that returns total size (sizeSf) of the real estate (locations) owned by who owns the most real estate (in terms of total size of locations owned by this person).
Question 1.3 (8 Points) 计算机mid代考
Write a query that returns pairs of suspects that have provided account suspecting each other of the same crime, e.g., in the example instance Bob is suspecting Peter to be the murderer of Alice while at the same time Peter is suspecting Bob to be her murderer. Make sure to return each such pair only once. Hint: (Bob,Peter) and (Peter,Bob) are the same pair of people.
Question 1.4 (10 Points)
Write a query that returns for each city the number crimes per type, e.g., the number of murders in London, the number of thefts in Windsor, and so on. For each city, crime type pair return how many of these crimes have been solved. A crime is considered solved if there is at least one account for this crimes and all accounts for that crime agree on the suspect. For example, in the example database the murder at Big Ben is not solved (contradictory accounts) whereas the theft at Windsor Castle is (one account cannot contradict itself).
Part 2 Relational Algebra (Total: 26 Points) 计算机mid代考
Question 2.1 Relational Algebra (6 Points)
Write an relational algebra expression over the schema from the SQL part that returns the time, type, and victim for all crimes in Windsor (the location city). Use the set semantics version of relational algebra.
Question 2.3 Relational Algebra (8 Points)
Write an relational algebra expression over the schema from the SQL part that returns cities where no crimes have been taken place so far (there was no crime in any location that is in this city). Use the set semantics version of relational algebra.
Part 3 Index Structures (Total: 24 Points)
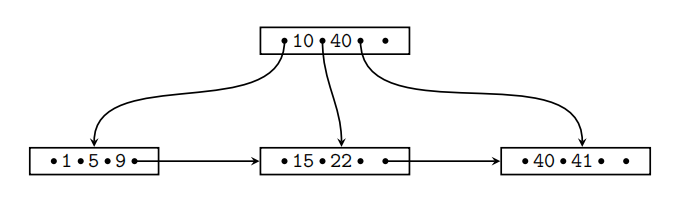
Question 3.1 B+-tree Operations (24 Points)
Given is the B+-tree shown below (n = 3 ). Execute the following operations and write down the resulting B+-tree after each step:
insert(6),insert(4),insert(3),delete(40) 计算机mid代考
When splitting or merging nodes follow these conventions:
- Leaf Split: In case a leaf node needs to be split, the left node should get the extra key if the keys cannot be split evenly.
- Non-Leaf Split: In case a non-leaf node is split evenly, the “middle” value should be taken from the right node.
- Node Underflflow: In case of a node underflflow you should fifirst try to redistribute and only if this fails merge. Both approaches should prefer the left sibling.
Part 4 I/O Estimation (Total: 18 Points)
Question 4.1 I/O Cost Estimation (12 = 4 + 4 + 4 Points)
Consider two relations R and S with B(R) = 100 and B(S) = 2, 000. You have M = 101 memory pages available. Compute the number of I/O operations needed to join these two relations using block-nested-loop join, merge-join (the inputs are not sorted), and hash-join. You can assume that the hash function evenly distributes keys across buckets. Justify you result by showing the I/O cost estimation for each join method.
Question 4.2 External Sorting (6 Points) 计算机mid代考
Consider a relation R with B(R) = 10, 000, 000. Assume that M = 101 memory pages are available for sorting. How many I/O operations are needed to sort this relation using no more than M memory pages.



