UNIVERSITY OF TASMANIA SCHOOL ENGINEERING
Filter Design代写 Design/Derive (determine the element values) for a N = 2 element equal-ripple filter if the ripple specification is 1.0dB
KNE488 RF Assignment (12.5%)
Due in Week 13
Filter Design
1.Design/Derive (determine the element values) for a N = 2 element equal-ripple filter if the ripple specification is 1.0dB. Do not use tables! Start with the definition of the power loss ratio. Prototype values only are required.Filter Design代写
![]()
With=1, the power loss ratio for the equal ripple filter is: 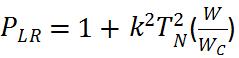
For the 2-element filter with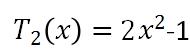 , we set up:
, we set up:
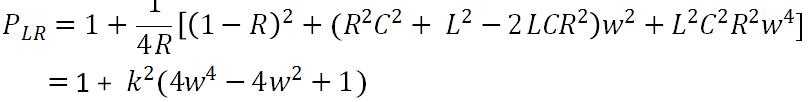
Which can be solved for R, L and C if the ripple level is knows. Thus, at w = 0, we have that:
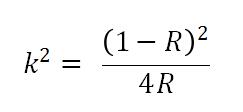
As we know, the ripple specification in the question is 1.0 db, the value of k can be derived as:
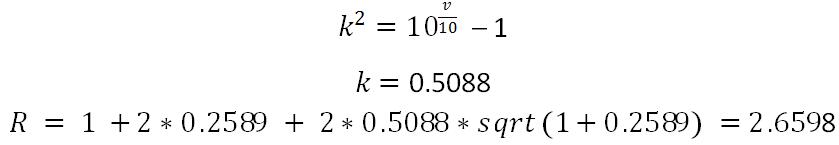
As we know,
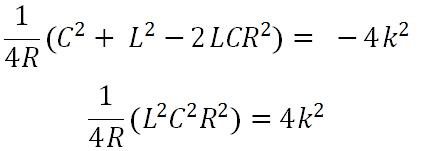
According to the equation above, we can derive the value:
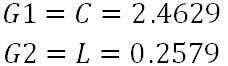
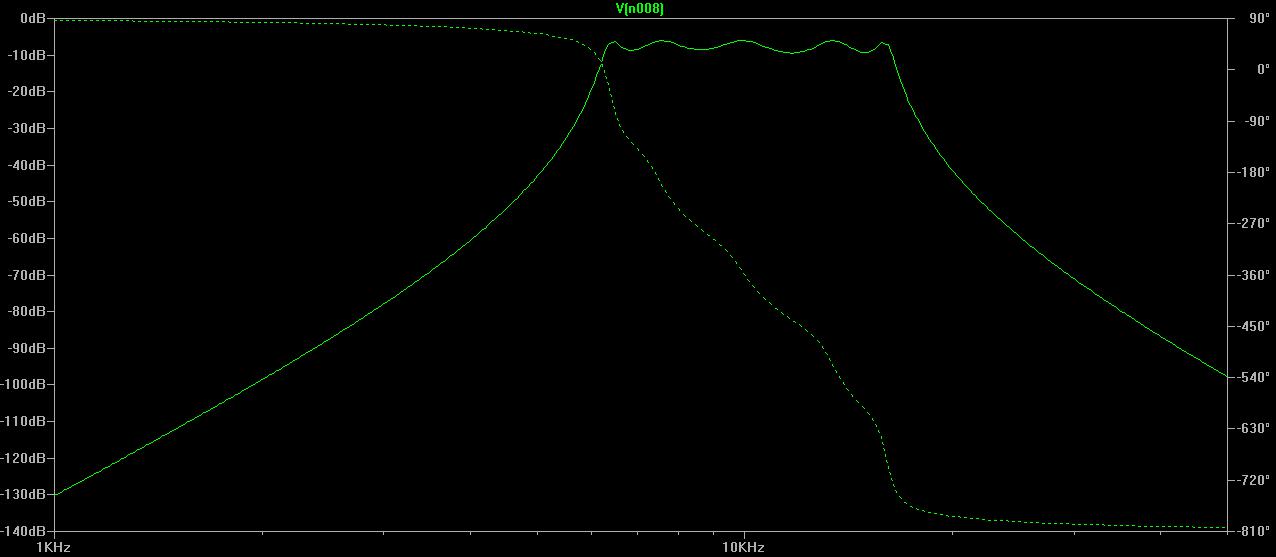
2.Determine the values of the reactive components (inductances and capacitances) for a 5th order 3dB bandpass Chebycheff filter with load and source impedances of 50Ω. The bandwidth is to be 4kHz, in this case, between 8kHz and 12kHz.
Low pass prototype: Filter Design代写
N g1 g2 g3 g4 g5 g6
5 3.4817 0.7618 4.5381 0.7618 3.4817 1.0000
L1 C2 L3 C4 L5 RL

3.Plot the frequency response (amplitude and phase) of question 2.
4.Determine the values of the reactive components (inductances and capacitances) for a 5th order low-pass-prototype with source and load terminations of 1 ohm for the following 3 cases:
a.Butterworth characteristic.
N g1 g2 g3 g4 g5 g6
5 0.6180 1.6180 2.0000 1.6180 0.6180 1.0000
b.Chebycheff 3dB characteristic.
N g1 g2 g3 g4 g5 g6
5 3.4817 0.7618 4.5381 0.7618 3.4817 1.0000
c.Bessel characteristic.
N g1 g2 g3 g4 g5 g6
5 0.9303 0.4577 0.3312 0.2090 0.0718 1.0000
5.Plot the frequency response of the 3 filters of Question 4 on a suitable frequency scale and compare and briefly discuss the different frequency responses.Filter Design代写
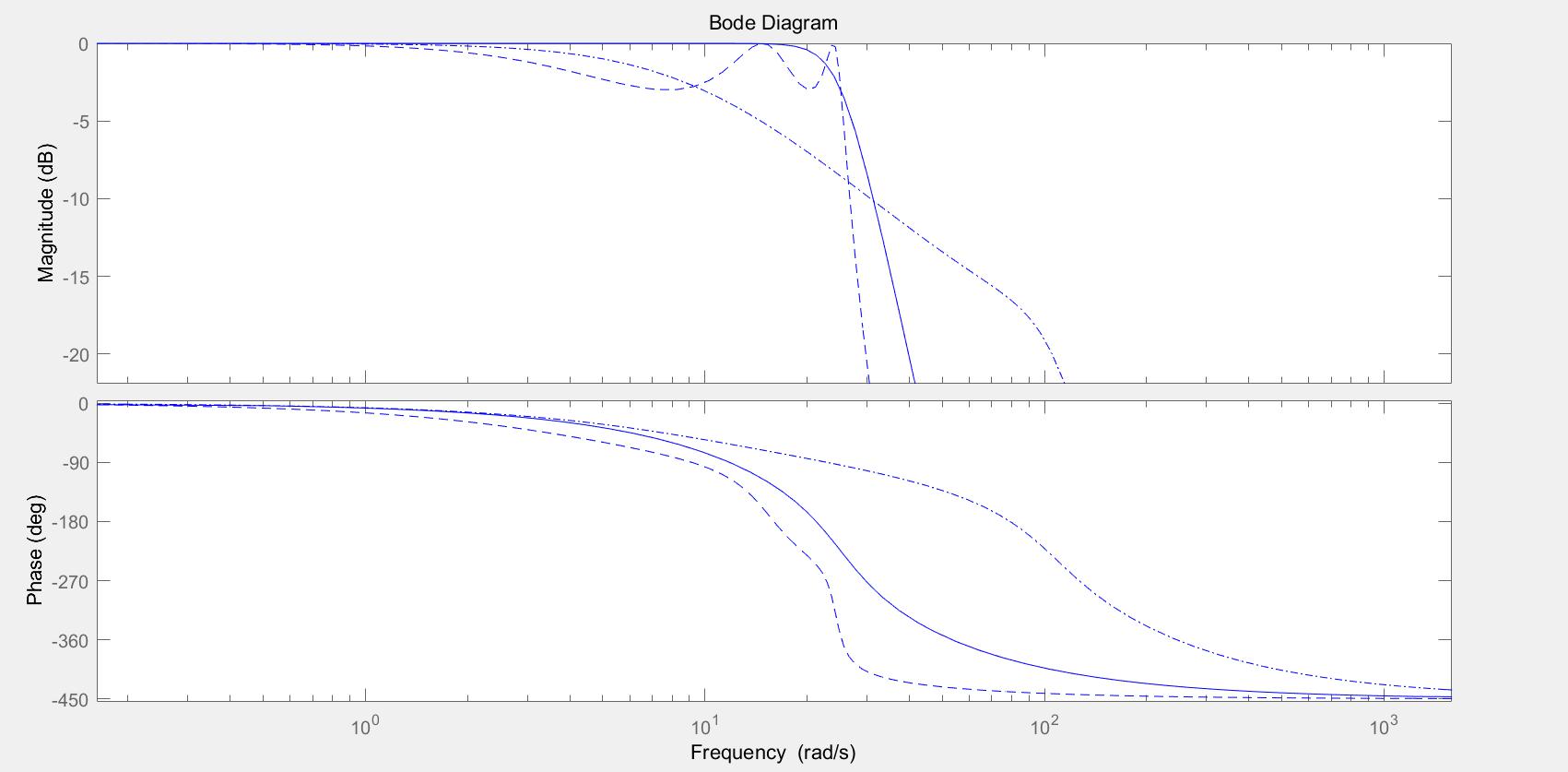
In the discussion, you may consider the following points:
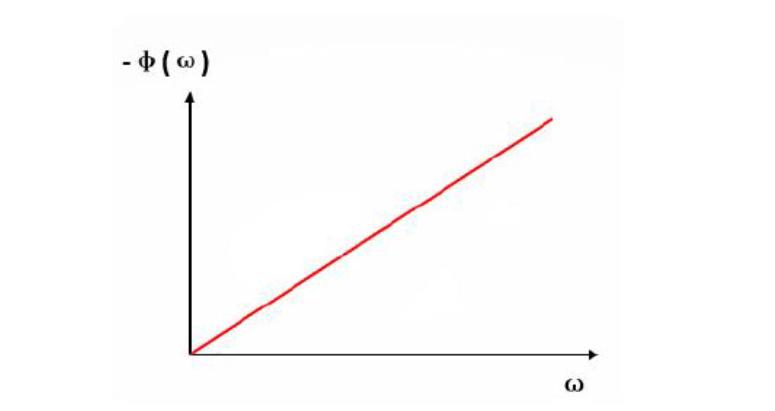
a.The Bessel filter values decrease monotonically, why?
Bessel Filters, modified for equiripple group delay, are frequently referred to as Linear Phase filters. The conventional linear filter is based on RC circuit, where the relationship between phase and frequency can be seen in the figure below. That’s why, in the passband, the filter values always decrease monotonically (linearly).
b.Compare the cutoff rates, phase responses and pass band attenuations between the filters.
The equal ripple response has the sharpest cutoff but the worst group delay characteristics. The maximally flat response has a flatter attenuation characteristic in the passband but a slightly lower cutoff rate. The linear phase filter has the worst cutoff rate but a very good group delay characteristic.
c.To compare the filters, you should normalize the attenuation magnitude to zero dB. State how this is done in the simulation and ensure that this is done for any comparison plots.
According to the power lose equation. Make sure when the w=0, there are no any power lose.
SPICE is a suitable tool for simulating the various filters.
更多其他:prensentation代写 Essay代写 Review代写 Resume代写 Report代写 Proposal代写 Capstone Projects 毕业论文代写 论文代写



您必须登录才能发表评论。