Strategic Decision Theory
Problem Set 10
金融作业代写 Consider the following method of dissolving a partnership. Two partners each own one share of a firm. They have a dispute…
Problem 1 金融作业代写
Consider the following method of dissolving a partnership. Two partners each own one share of a firm. They have a dispute and each partner wishes to either buy-out, or be bought- out by the other partner. Partner i values both his own and his partner’s share at θi per share. Assume that the θi ’s are independently and uniformly distributed on [0,1]. Each partner knows his own θ but not his partner’s. The mechanism that the partners agree upon is the following:
Each partner bids for the other’s share. The highest bidder wins and obtains her part- ner’s share for the amount of her winning bid. In the event of a tie, each partner wins with equal probability. 金融作业代写
(a) Solve for a symmetric equilibrium bidding function in linear strategies, that is, of the form:
bˆ (θ ) = α + βθ
Is such an equilibrium unique?
(b) Suppose the mechanism was modified as follows: The highest bidder wins the oppo-nent’s share but pays the amount of the losing Solve for a symmetric linear equi- librium b˜ ( ). Discuss whether b˜ ( ) exceeds, equals, or is less than bˆ ( ); of course, this relationship may vary with θ .
(c) Formulate a revenue equivalence result for this environment and briefly sketch a proof.
Problem 2 金融作业代写
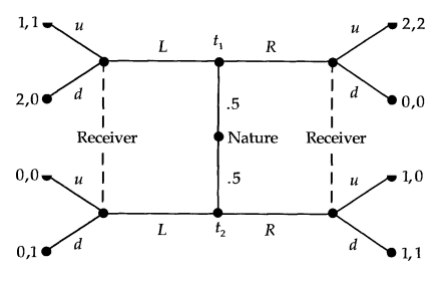
Find all pure strategy perfect Bayesian equilibria (both separating and pooling) of the fol- lowing signaling games. Nature draws a type, the sender acts, the receiver sees the action (but not the sender’s type) and responds.
- Gibbons3.b (page 247).
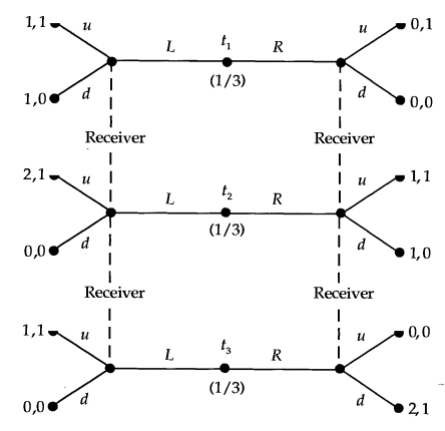
- Gibbons4.a (the upper one on page 248).