MATH96054 Stochastic Simulation
随机模拟代写 (i) What is the defifinition of a pseudo-random number? (ii) Explain the importance of pseudo-random numbers in stochastic simulation.
-
(a) (i) What is the defifinition of a pseudo-random number? (1 mark)
(ii) Explain the importance of pseudo-random numbers in stochastic simulation. (1 mark)
(b) Defifine the following concepts
(i) Congruential multiplicative generator and congruential mixed generator. (2 marks)
(ii) Period, Full period and Maximal period for congruential generators. (3 marks)
(c) Write down the recursion for the congruential generator with the parameters: (5 marks)
seed = 1, modulus = 343, shift = 3, multiplier = 53;
and establish whether or not it has full period. Provide a detailed statement of any results used to justify your answer. 随机模拟代写
(d) Consider the following R code
MyCGen <- function(x0,a,b,alpha,n){
x <- c(x0,rep(0,n-1))
for(i in 1:(n-1)){
x[i+1] <- ((b + a*x[i]) %% (2**alpha))
}
if ((x0 %% 2) != 0 && ((a %% 8 == 5 ) || (a %% 8 == 3)))
cat("The period of the generator is = ", format(*****),"\n")
return(x)
}
(i) Describe the value(s) in x returned by the following R code (1 mark) 随机模拟代写
MyCGen(x0, a, b, alpha, n).
(ii) Suppose that the function MyCGen is called with the following parameters: (3 marks)
MyCGen(7, 35, 0, 20,100)
What code should replace ***** to guarantee that the function displays the period of the generator correctly? Justify your answer.
(iii) Assuming **** returns the correct period for the parameters in part (ii) and suppose that the function is called with the following parameters: (2 marks)
MyCGen(3, 21, 2, 10,100)
What period is displayed by the function? Do you agree with the result? Justify your answer.
(iv) What would be your answer to Part (iii) if the function is called with the following parameters (2 marks)
MyCGen(11, 21, 0, 3,100)
(Total: 20 marks)
(a) Consider a random variable X with density fX(x) = Cx−(β+1) , x ≥ 1, for some appropriate constant C and β > 0.
(i) Determine the value of the constant C. (1 mark)
(ii) Can the inversion algorithm be used to sample random variates with distribution determined by the function density fX(·)? Justify your answer. (1 mark)
If an inversion scheme can be used, provide the missing code ***** in the R code below so as to guarantee that the function GenX returns random variates with density function fX(·). (2 marks) 随机模拟代写
GenX < - function(n,beta)
{
U <- runif(n)
X <- *****
return(X)
}
(iii) Assume that the parameters x0, a, b, alpha and n are given. If one is interested in using pseudo-random numbers generated by the function
MyCGen(x0, a, b, alpha, n)
as defifined in 1(d) above, what is the R code that needs to replace the line U <- runif(n) in the function GenX defifined in 2(a)(ii) above? Justify your answer. (2 marks)
(b) (i) Suppose you are given an arbitrary function f : R → R. Provide the main assumptions that you would need to verify to ensure a valid rejection scheme exists to sample from f. (4 marks)
(ii) Defifine the acceptance region CfX determined by a density function fX when using the ratio-of-uniforms scheme. What are the assumptions you would verify on fX to ensure that you can bound CfX within a rectangle? Justify your answer. (2 marks)
Question 2 随机模拟代写
(c) (i) Given the following code
MyFunc <- function(n,a,b)
{
x <- vector("numeric")
count <- 0
while (count < n){
u <- 2*runif(n)-1
v <- 2*runif(n)-1
w <- u*u + v*v
wa <- w[w<=1]
x<- c(x,sqrt((-2*log(wa))/wa)*u[w<=1],
sqrt((-2*log(wa))/wa)*v[w<=1])
count <- length(x)
}
x <- a + b*x[1:n]
return(x)
}
Determine the distribution of the output vector and provide the algorithm of the simulation method used to design the R code above. (3 marks)
(ii) Explain in detail the crude Monte Carlo method to estimate integrals. (2 marks)
(iii) Let Y be a standard normal random variable, i.e. Y ∼ N(0, 1). Denote by FY (·) the probability distribution of Y . Providing all the details, give a Monte Carlo estimator of FY (y), for any arbitrary y ∈ R and write down the algorithm. (3 marks)
(Total: 20 marks)
3. (a) Let Z be a random variable with a standard normal distribution. Give the Importance Sampling estimator for P(Z ≥ 4) by using a uniform distribution as a sampling distribution. 随机模拟代写
Hint: Use a change of variables. (3 marks)
(b) (i) Explain the general idea of the Markov Chain Monte Carlo (MCMC) methods seen in lectures and their main drawback in the context of Monte Carlo estimators. (2 marks)
(ii) State the detailed-balance criterion for Markov Chains and explain its importance in the context of the MCMC methods. (2 marks)
(c) (i) Let X be a random variable in R. Given X = x, defifine Y = x + Z, where Z ∼ N(0, 1). What is the distribution of Y |X = x? (1 mark)
(ii) Let Q(·|x) be the conditional density function of Y |X = x as defifined above. Using Q(y|x) as a transition kernel, outline an MCMC algorithm (and justify your choice) to sample random variates X with density function
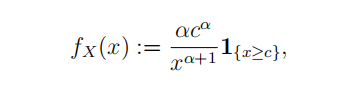
where c > 0 and α > 0. (4 marks)
(iii) Using the same proposal transition density Q(y|x), outline the Metropolis algorithm to sample from a density function (2 marks)
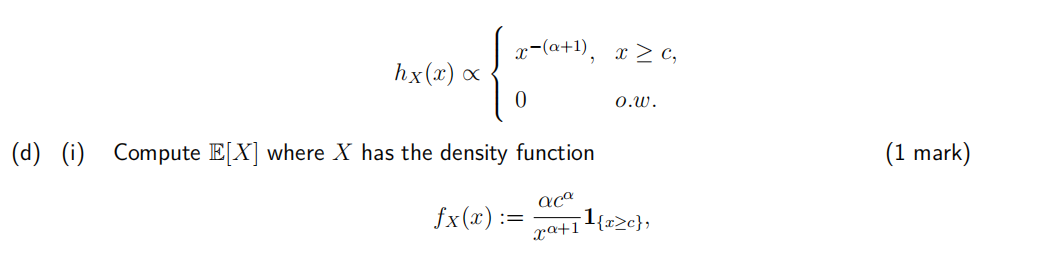
where c > 0 and α > 0.
(ii) Suppose now that you have a sample of random variables X1, . . . , Xn obtained from your MCMC algorithm outlined in (c)(ii) above.
(ii.a) What potential issues may there be if you use the sample to obtain a Monte Carlo estimate of E[φ(X)] for appropriate functions φ? Justify your answer. (2 marks)
(ii.b) Can you provide an estimator for E(X) using the sample from your MCMC algorithm above? If so, give the estimator detailing any conditions on the parameters c and α such that your estimator is valid. (3 marks)
(Total: 20 marks)



