Practice Questions for Mid Semester Test
BFF5340 – Advanced Derivatives
高级衍生品代考 For each of the statements below, state whether it is TRUE or FALSE and EXPLAIN the reason.
Question 1 (Past exam question)
For each of the statements below, state whether it is TRUE or FALSE and EXPLAIN the reason.
1) When a stock’s continuously compounded rate of return is described as following Geometric Brownian Motion, it is known that the expected rate of return of the stock must be the risk-free rate, and that the stock’s returns are independent and normally distributed over time, implying that the variance of return increases as a function of the square root of time. 高级衍生品代考
Type answer here
2) An option promises to pay the holder $10 if a non-dividend paying stock decreases below its current price of $100 to less than or equal to $80 at the end of 24 months. The risk-free rate of return is 5% per annum, continuously compounded and the volatility of the stock’s return is 30%. Under the Black-Scholes-Merton framework, the risk-neutral probability of receiving cash at maturity is 29.13%.
Type answer here
3) In the Black-Scholes-Merton framework, the price of a forward start option with the strike price being a known multiplier of the spot price when the option comes into existence, is always the same as the price of the equivalent option that starts immediately.
Type answer here
(3 × 5 = 15 marks)
Question 2 (Past exam question) 高级衍生品代考
a) What is the evidence indicating that the Black-Scholes-Merton model does not accurately price European options in the real world? What is the reason behind this “failure”?
Type answer here.
b) On October 12, the S&P 500 index (SPX) was trading at 3,477.13. The price of a put option on the index expiring on December 4 with strike of 3300 is 71.67.
i. Assuming the risk-free interest rate for that period is 0% p.a., the annual dividend rate on the SPX is 1.75%, and there are 40 working days over that period (so you can use T=40/252), compute the implied volatility for the option.
Answer this question in Excel. Name the worksheet as ImpliedVolatility.
ii. Now consider another put option on the SPX also expiring on December 4, with a strike price of 3200. State whether the implied volatility for this option is expected to be greater than, equal to, or less than the one computed in (i). Briefly explain your response.
Type answer here.
(5+6+4=15 marks)
Question 3 高级衍生品代考
In no more than 6 sentences, explain how the BSM partial differential equation is derived and how it then leads to the BSM option pricing formula.
Type answer here.
Question 4
An option on a stock is said to be at-the-money-forward (ATMF) if the strike price equals the forward price on the stock for that maturity. Assume there are no dividends, so the ATMF strike is K = S0e rT. Show that according to the Black-Scholes-Merton model, the value of an ATMF call is given by
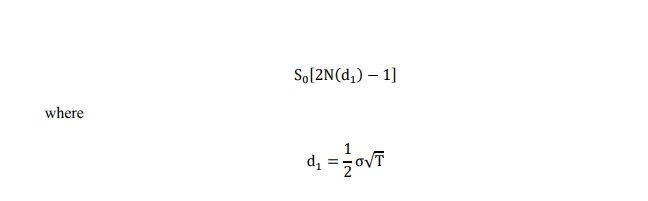
Type or insert screenshot of answer here.
Question 5
Which of the following is true when the stock price follows geometric Brownian motion
A. The future stock price has a normal distribution
B. The future stock price has a lognormal distribution
C. The future stock price has geometric distribution
D. The future stock price has a truncated normal distribution
Question 6
What does N(x) denote?
A. The area under a normal distribution from zero to x
B. The area under a normal distribution up to x
C. The area under a normal distribution beyond x
D. The area under the normal distribution between -x and x
Question 7 高级衍生品代考
Which of the following is NOT true?
A. Risk-neutral valuation provides prices that are only correct in a world where investors are risk-neutral
B. Options can be valued based on the assumption that investors are risk neutral
C. In risk-neutral valuation the expected return on all investment assets is set equal to the risk-free rate
D. In risk-neutral valuation the risk-free rate is used to discount expected cash flows
Question 8
A variable x follows the stochastic process ?? = ??? + ??? in which a and b are constants and
?? is a Wiener process. Consider variable ? = ??.
i. Using Ito’s lemma, derive the process for ?.
ii. In the Black-Scholes-Merton model, what variables do x and y correspond to?
Question 9 高级衍生品代考
A stock price is currently $30. Its volatility is 20%. The risk-free interest rate is 5 percent per annum with continuous compounding. In Excel, using a five-period Cox-Ross-Rubinstein binomial tree, compute the value of a 1-year European put option with a strike price of $30.
Question 10
Why do you think it is important to set the exit point in advance when trading?



