数学代考 Final Assignment for MA 412

Final Assignment for MA 412, Spring 2020

数学代考 This assignment will serve as your final exam. It is optional for anyone content with a “Credit/NoCredit” grade or a letter grade…

Purpose: This assignment will serve as your final exam. It is optional for anyone content with a “Credit/NoCredit” grade or a letter grade of C or lower. It is required for anyone wanting a letter grade of B- or higher. The purpose of the assignment is to give you an opportunity to demonstrate to me the extent to which you have learned the material from the course.

Assignment: In order to try for a grade of B- or higher, you much chose one topic from each of the groups (i), (ii), and (iii) below and write about all three of them in 8-10 double-spaced pages total. In order to try for a grade of A- or A, you must additionally chose one proof from each of the groups (a) and (b) and write about them both in 4-5 total additional double-spaced pages. The proofs in group (a) aregiven in the book, so you just need to demonstrate a sufficient understanding of the proof(s). Group (b) consists of statements for you to prove yourself. Any student content to try only for a grade of B-, B, or B+ need not complete the additional task of writing about the proofs.

Group (i): 数学代考

• Rootsof equations of the form zⁿ = w and az² + bz + c = 0, with a, b, c, w ∈ C fixed and n a positive integer.
• Limits and continuity.
• Differentiability and the Cauchy-Riemann equations.

Group (ii):

• M¨obius Transformations and the Riemann Sphere.
• Cauchy’s Theorem.
• Cauchy’s Integral Formula.

Group (iii):

• Power series and regions of convergence.
• Taylor and Laurent Series.
• Classification of Singularities.
• The Residue Theorem

Group (a): 数学代考

• Proof of the Cauchy-Riemann equations (Theorem 13, both parts)
• Proof of Cauchy’s Theorem and the Cauchy Integral Formula (Theorem 18 and Theorem 4.24)
• Proof(s) of the Fundamental Theorem of Algebra (Theorem 11; Proof 1 is just after the statement of Theorem 5.11 and proof two is just after Corollary 5.13. See also Exercises 8.15 and 9.22)
• Representationof a holomorphic function via power series (Theorems 1 and 8.8)
• Proof of the results characterizing thetypes of singularities (Proposition 9.5 and Theorem 9.7)

Group (b):

• Let{a_n} be a (complex)  A point a ∈ C is said to be an accumulation point of the sequence if for every ϵ > 0 and N ∈ N ∃ n > N such that |a_n − a| < ϵ. Prove that if a sequence has more than one accumulation point it must be divergent.
• Let{ƒ_n} be a sequence of functions that are holomorphic in a region G and suppose that {ƒ_n} converges uniformly to a function ƒ on G. Prove that ƒ is holomorphic in G.

• Provethat there exists an R ∈ [0, ∞] such that the Laurent series

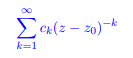
converges for 数学代考

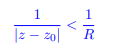
and  that  the  convergence  is  uniform  on  {z  ∈ C :  |z − z₀| ≥ r} for  any  fixed  r  >  R.   What  is  the smallest value R can take?

• Supposeƒ is a nonconstant entire  Prove that, given any w ∈ C and any ϵ > 0, ∃ z ∈ C such that |ƒ (z) − w| < ϵ.

Formatting: If you know tex (the standard way to write mathematics), please use it. If you would like to use this as an opportunity to learn tex, I would be happy to help you do that. If you do not, feel free to use any standard text editor (eg Google Docs, Word, etc). The paper should be largely expository. So you should not need to use a large number of special symbols or equations. When you would like to refer to an equation or figure, you can write/draw those by hand, include them at the end of your submission. 数学代考

And refer to them in the main body of your paper. Those of you submitting a proof for group (b), since you will be writing this proof yourself, please feel free to write this out by hand, take a picture of it. And include it in your submission that way. Please make sure your submission is a single .pdf file; append any necessary photos of hand written/drawn components to that single .pdf file.

Due Dates: Complete assignment due by noon (Boston time) on Thursday, April 30. This deadline is firm. No late papers will be accepted. If you would like to receive comments on a (partial) draft, please submit the (partial) draft no later than 8am (Boston time) on Monday, April 13. I strongly suggest that you submit a draft for comments. Think of the submission of the draft as your second midterm.

Comments:

• For groups (i) through (iii), the idea is to explain these largely in words, not symbols, and explainboth what the concept is, why it is useful and/or interesting, and maybe also how it relates to concepts in R2. If you are able to identify a common theme, idea, teachnique, etc that is relevant for all the topics you choose, that would be a potentially interesting thing to discuss.
• For groups (a) and (b), ideally you would describe not just the method of proof. But also the intuition behind the method and the intuition behind why the result is true. 数学代考

• Do not just paraphrase the book (or another book that you find online). It is important that you add your own insight and perspective to the concepts/proofs.

• I realize this assignment might feel very new to you and like nothing you’ve done before for a math class. Being able to explain mathematics via written communication is a fundamental skill in mathematics that tends not to be emphasized in most undergraduate curriculums, for reasons which are not entirely This skill is important not just within the mathematics community itself. But also for any job or career that involves mathematics. Imagine, for example, that you have been asked to solve a problem for your company and then asked to present that solution in a written report. Your colleagues would need to be able to understand your method, and its importance, just by reading that report.
• I often find that I don’t truly understand something until I try to explain it to someone else. Or until I try to “explain it to myself” by writing it down.  If you are unsure of how to explain any of the above concepts/proofs, that likely means you don’t fully understand them. 数学代考
• It is ok for you to generally discuss with others the topics that are relevant for this However, the paper you submit should be written by you, in your own words. If you choose to complete parts (a) and (b), please do not discuss the proofs in part (b) with anyone. Treat the problem you choose for part (b) as an open-book, take-home exam.