Time Series Analysis
Coursework 2
时间序列代写 This coursework is worth 5% of your mark for Time Series Analysis. There are 3 questions and a total of 20 marks available.
This coursework is worth 5% of your mark for Time Series Analysis.
There are 3 questions and a total of 20 marks available.
You may use any results from the notes you wish, but you must properly cite them.
You may use MATLAB, R or Python, however I strongly recommend using MATLAB.
You must type it up (MS Word or LATEXis fine), including all your code within the main text (not as appendices or screen shots), and submit a pdf.
Your report must be no more than 10 pages (not including a cover page).
NB: Stationarity by itself always means ‘second-order’ stationarity. 
denotes white noise with mean zero and variance 
Assume is Gaussian/normal here.
Question 1 (2 marks) 时间序列代写
Write a function S_AR(f,phis,sigma2) that evaluates the parametric form of the spectral density function for an AR(p) process at a designated set of frequencies. The inputs should be:
f: the frequencies at which to evaluate the spectral density function;
phis: the vector [φ1,p, …, φp,p];
sigma2: the variance of the white noise.
Your function should not take p as an input, but instead determine it from the stated input parameters.
Question 2 (8 marks)
For a portion X1, …, XN of a zero mean stationary random process {Xt}, the periodogram is defined as
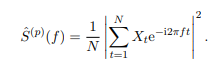
Asymptotically as N → ∞
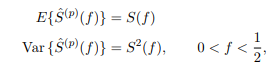
where S(f) is the spectral density function of {Xt}. 时间序列代写
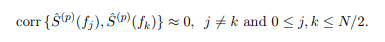
If we restrict ourselves just to the Fourier frequencies fk = k/N, we also find that the (N/2)+1 random variables (N even), Sˆ(p)(f0), Sˆ(p)(f1), . . . , Sˆ(p)(fN/2), are all approximately pairwise uncorrelated for N large enough; i.e.,
Consider the following sequence of tasks (A)-(C) for some N (divisible by 4):
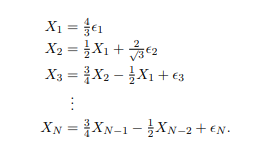
(A) Use a Gaussian random number generator to create a realisation of a portion E1, E2, . . . , EN of a Gaussian white noise process with zero mean and unit variance. Generate a corresponding realisation of a portion X1, X2, . . . , XN of the zero mean AR(2) process 
To do this generate: 时间序列代写
(The first two values are structurally different to the rest in order to avoid “start-up” transients which would occur if we just set X1 = X2 = 0).
(B) Using X1, …, XN , compute the periodogram at the Fourier frequencies, making use of the fft1 function.
(C) Repeat steps (A)-(B) a total of Nr = 10000 times, storing the sequences 
Perform steps (A)-(C) for N = 4, 8, 16, 32, 64, 128, 256 and 512. Using your sequences, produce the following three plots on separate axes and give a brief comment on them.
(a) The sample mean of 
(y-axis) against N (x-axis). Plot a horizontal line to show the large sample result for the mean given above.
(b) The sample variance of (y-axis) against N (x-axis). Plot a horizontal line to show the large sample result for the variance given above.
(c) The sample correlation coefficient ˆρ (the Pearson product moment correlation coefficient) between and 
(y-axis), against N (x-axis). Plot a horizontal line to show the large sample result for the correlation given above.
Question 3 (10 marks) 时间序列代写
You each have your own individual AR(4) time series of length 128 which can be retrieved by downloading
wwwf.imperial.ac.uk/~eakc07/time_series/number.csv,
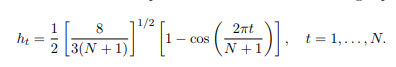
where instead of number you insert the number next to your name in time_series_number.pdf on blackboard.
You can assume your time series has a mean of zero.
(a) (i) Write your own code for the direct spectral estimator with a Hanning taper, defined here
(ii) Compute the direct spectral estimate for your time series and plot it.
(b) (i) Write your own code for fitting an AR(p) model using the tapered Yule-Walker scheme, utilising the Hanning taper.
(ii) Using your code, fit an AR(4) process and state the estimates of the unknown parameters to 4.d.p..
(iii) Plot the corresponding tapered Yule-Walker estimate for the spectral density function. 时间序列代写
(c) (i) Write your own code for fitting an AR(p) model using the forward least-squares scheme.
(ii) Using you code, fit an AR(4) process to the (untapered) data and state the estimates of the unknown parameters to 4.d.p..
(iii) Plot the corresponding forward least-squares estimate for the spectral density function.
(d) In no more than 100 words, comment on your figures, making inference on the random process that generated your time series.
