1The relationship between blood alcohol content and age

alcohol content代写 Check model diagnostics, and when you are happy, concisely report and interpret the results of your model
1.1Check model diagnostics, and when you are happy, concisely report and interpret the results of your model alcohol content代写
Comment:
From the figure 1, we could see the line in residuals vs fitted plot are horizontal, which showed that the assumptions of Linear is met.
From Normal Q-Q in Figure 1, we could find the few points are far from the 45 degree line which indicates the assumptions of Normality is not met, but most points fall on the 45 degree line which imply the assumptions of Normality is met, thus we conclude the assumptions of Normality have been met .alcohol content代写
From Scale-Location in Figure 1, we could see that the points around the horizontal line distribute randomly, thus we conclude the assumptions of equal variance have been met.
From the figure 2, we could see that age have negative effect on Blood Alcohol Content (%) as measured by breathalyser, which are significant since the p values of age is less than 0.05. The estimate of age is -0.143. It means Blood Alcohol Content decreases 0.143 % when age increase 1 year.
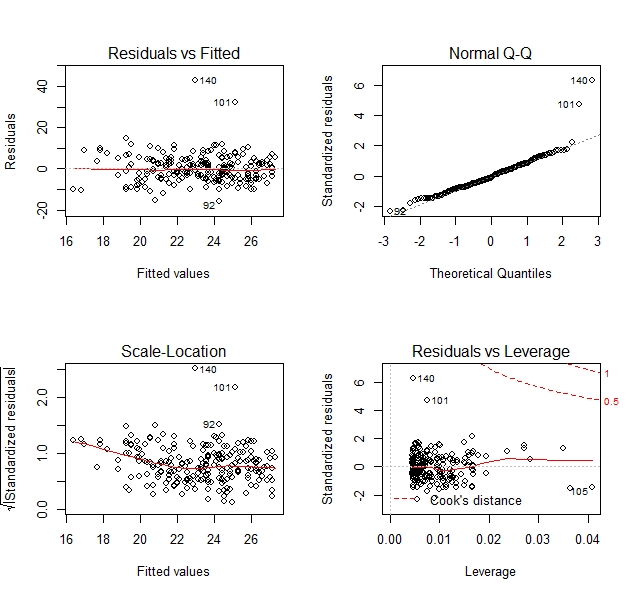
Figure1 Model diagnostics
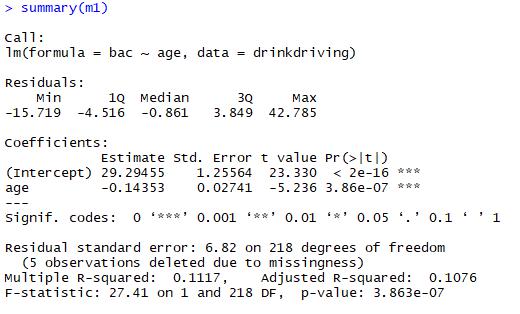
Figure2 the results of model
1.2What is the predicted blood alcohol content for a 50 year old driver who gets stopped by the Police?
Comment:
From the figure 3, we could see the predicted blood alcohol content for a 50 year old driver who gets stopped by the Police is 22.118%.alcohol content代写
![]()
Figure3 the results of prediction
1.3Produce and interpret a diagnostic plot of the model that shows whether or not the model residuals are normally distributed.
Comment:
From Figure 4, we could find the few points are far from the 45 degree line which indicates the assumptions of Normality is not met, but most points fall on the 45 degree line which imply the assumptions of Normality is met, thus we conclude the assumptions of Normality have been met .
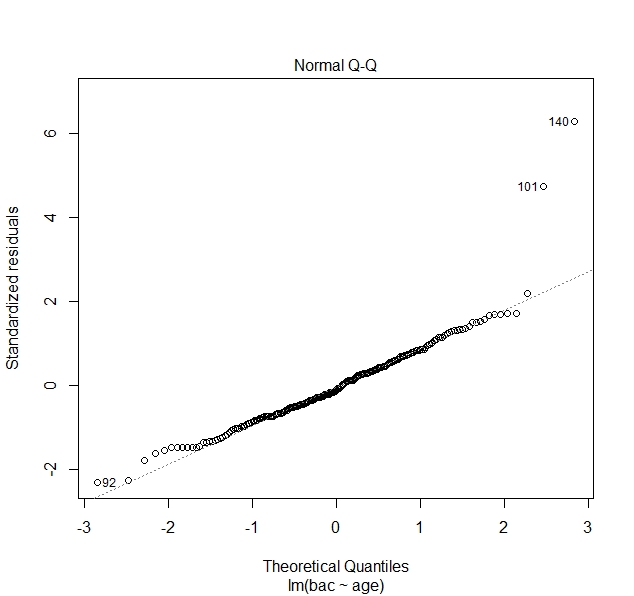
Figure4 diagnostic plot for normally distributed
2.Driving speeds, night vs. day
2.1Does either time of day or speed of driving predict the blood alcohol content over and above their age? Fit appropriate model(s) to test this question.
Comment:
From Figure5, we could find that the speed and nighttime have positive effect on Blood Alcohol Content (%) as measured by breathalyzer over and above their age, which are significant since the p values of speed and nighttime are less than 0.05.
The estimate of speed and nighttime is 0.198 and 3.846, respectively.
It means Blood Alcohol Content increases 0.198 unit when speed increase 1 unit.
Blood Alcohol Content when the incident occurred at night increases 3.846 unit compared with that at day.
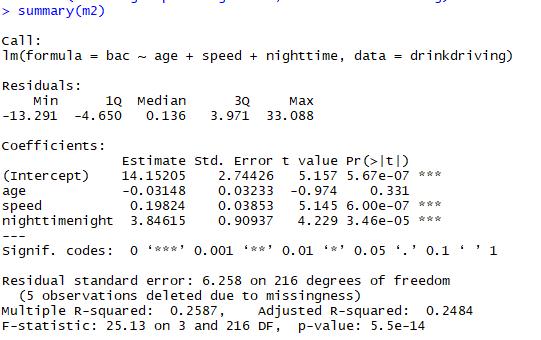
Figure5 the result of model 2
2.2Run model diagnostics and, if needed, re-fit the model(s). How much variation in blood alcohol content is accounted for by drivers’ ages and speeds, and time of day of incidents?
Comment:
From Residuals vs leverage in Figure 6, we could see that the points 140 and 101 may be the outlier. So we delete those observations and refit model.
From the figure 7, we could see the line in residuals vs fitted plot are horizontal, which showed that the assumptions of Linear is met.
From Normal Q-Q in Figure 7, we could find the few points are far from the 45 degree line which indicates the assumptions of Normality is not met, but most points fall on the 45 degree line which imply the assumptions of Normality is met, thus we conclude the assumptions of Normality have been met .
From Scale-Location in Figure 7, we could see that the points around the horizontal line distribute randomly, thus we conclude the assumptions of equal variance have been met.
The variations in blood alcohol content were showed in Figure 8.alcohol content代写
Variation in blood alcohol content is 18.341 % accounted for by drivers’ ages.
Variation in blood alcohol content is 1.969 % accounted for by drivers’ speeds.
Variation in blood alcohol content is 7.595 % accounted for by time of day of incidents.
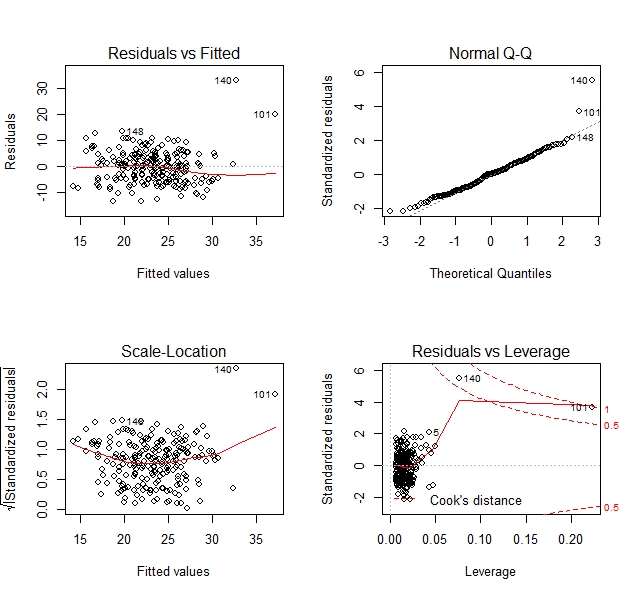
Figure6 Model diagnostics of model 2
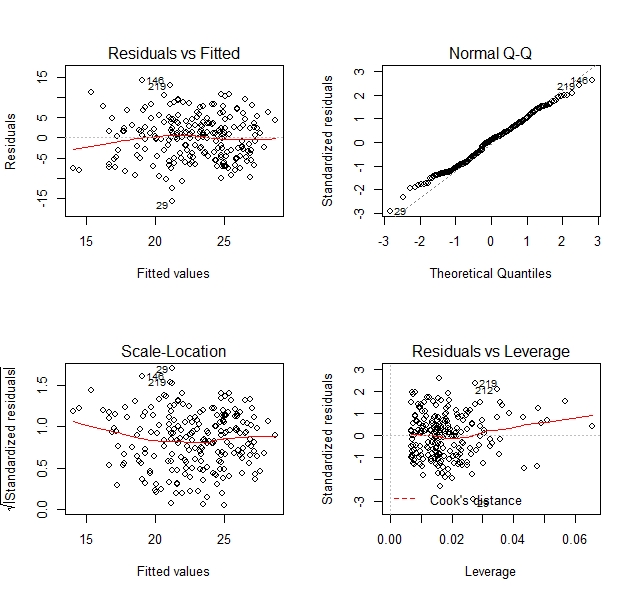
Figure7 Model diagnostics of model 3

Figure8 Variation in blood alcohol content is accounted for by drivers’ ages and speeds, and time of day of incidents
2.3Is there evidence to suggest that people drive faster at night than during the day?
Comment:
From Figure9, we could find that the nighttime have not significant effect on speed, which are not significant since the p values of nighttime are greater than 0.05. Thus, there is no evidence to suggest that people drive faster at night than during the day.
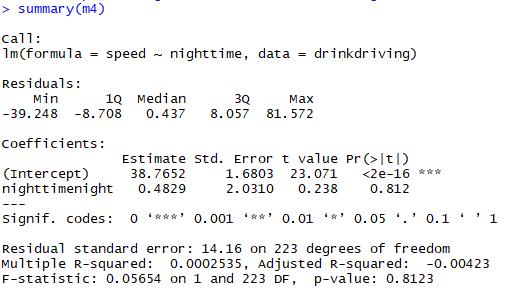
Figure9 the results of model 4
Fines vs. Warnings
3.1 Construct a model to investigate what contributes to the likelihood of a driver receiving a fine as opposed to a warning.alcohol content代写
Report the results of your model.
What has the biggest effect on the likelihood of receiving a fine, 1~SD increase in driving speed or 1~SD increase in blood alcohol content?
Comment:
From the Figure10, we could find that the p-value of variable speed, Blood Alcohol Content and age were less than 0.05, so we could accept that the probability of a driver receiving a fine as opposed to a warning was different in different speed, Blood Alcohol Content and age.
The coefficient of age is negative, so we could conclude that age may have negative effect on the probability of a driver receiving a fine. It means the young driver has high probability to get fine.
The coefficient of speed and Blood Alcohol Content are positive, so we could conclude that speed and Blood Alcohol Content may have positive effect on the probability of a driver receiving a fine. It means the driver with high speed and Blood Alcohol Content has high probability to get fine.
From the Figure11, we could find that 1~SD increase in driving speed has the bigger effect (10.42) on the likelihood of receiving a fine, than that in 1~SD increase in blood alcohol content (7.175).
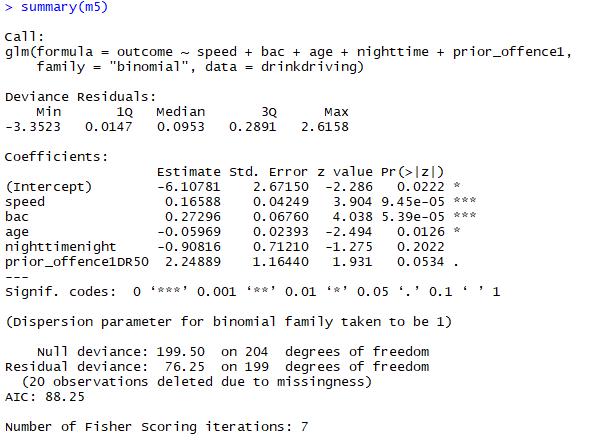
Figure10 the results of model 5

Figure11 the likelihood of receiving a fine
3.2 Are people with prior convictions for drink driving offences more likely to get a penalty fine (as opposed to a warning) than those who have non-drink-related offences?
Comment:
From the Figure12, we could find that the p-value of prior_offence1DR50 was greater than 0.05, so we could not accept that the probability of a driver receiving a fine as opposed to a warning was different in different prior convictions.
The coefficient of prior_offence1DR50 is positive, so we could conclude people with prior convictions for drink driving offences are more likely to get a penalty fine (as opposed to a warning) than those who have non-drink-related offences but it is not significant.

Figure12 the results of model 6
3.3 Does whether or not a driver has a prior motoring offence (of any kind) influence the likelihood of receiving a fine?
Comment:
From the Figure13, we could find that the p-value of prior_offence2Motoring offence was greater than 0.05, so we could not accept that the probability of a driver receiving a fine as opposed to a warning was different in different prior convictions.
The coefficient of prior_offence1 Motoring offence is positive, so we could conclude people with prior motoring offence (of any kind) are more likely to get a penalty fine (as opposed to a warning) than those who have non- related offences but it is not significant.

Figure13 the results of model 7
4 Plotting predicted probabilities
Comment:
The predicted probabilities were presented in Figure 14.
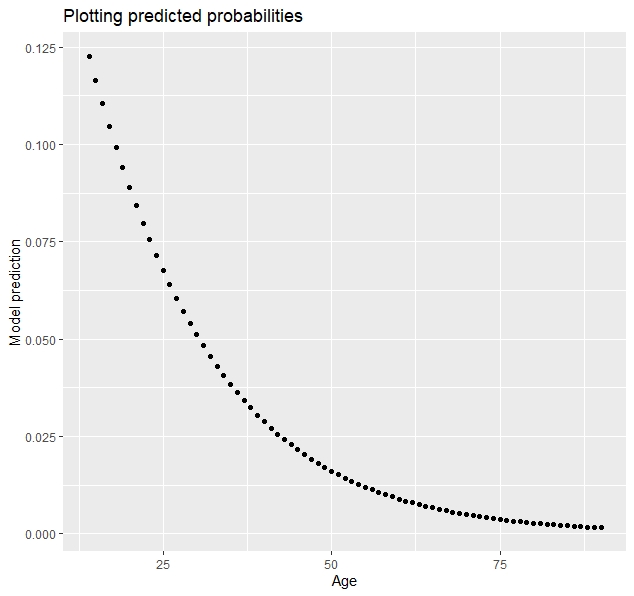
Figure14 predicted probabilities
5 Corrupt cops?
Investigate the hypothesis that one of the police officers is biased in how the give out fines and warnings with respect to a driver’s age.
Does the data suggest that this might be the case? If so, which police officer(s) is biased, and how?
Comment:
We observed the interaction of each police officers and driver’s age by setting different comparison groups of dummy variables in order to investigate the hypothesis. For example, when we set the AS officer as comparison group, then the coefficient of age stand for the effect on the AS officer give out fines and warnings with respect to a driver’s age.
From the Figure15,16 and 17, we could see that police officers are easy to give fine to young driver and it is significant since the p value were less than 0.05.
From the Figure18, we could find that the AS officer have high absolute coefficient among police officers, which means AS officer may have high bias, and because the coefficient is negative, which means AS officer is easy to give fine to young driver.
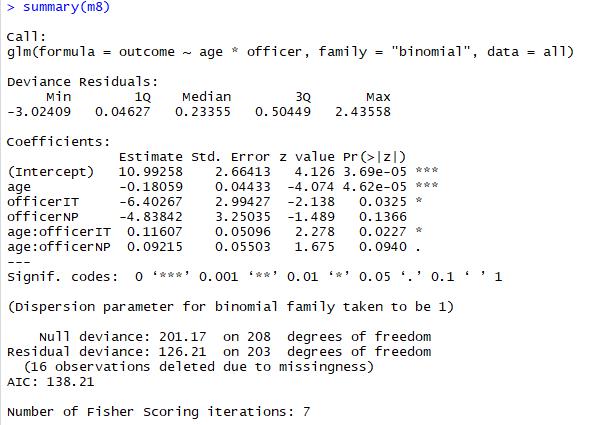
Figure15 the results of model 8
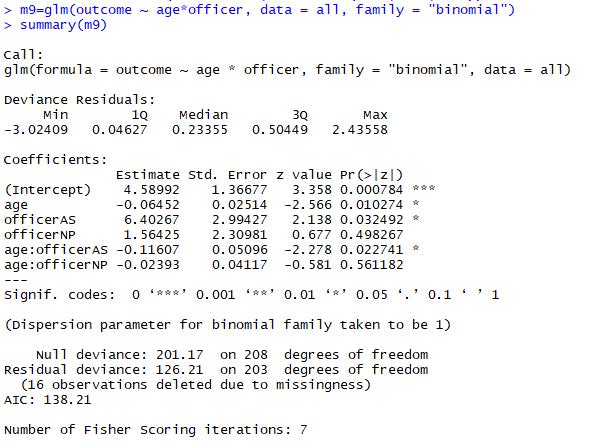
Figure16 the results of model 9
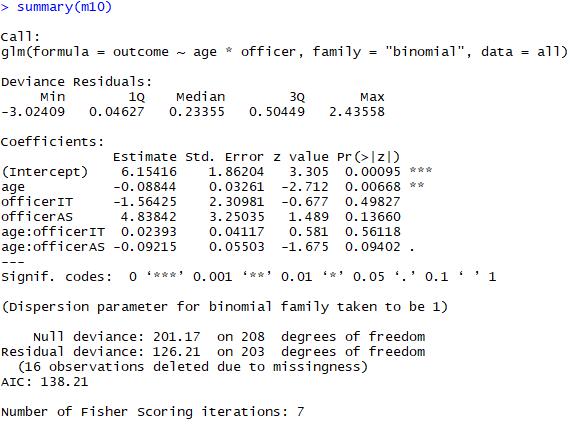
Figure17 the results of model 10

Figure18 the results of coefficient of officer give out fines and warnings with respect to a driver’s age

更多其他:prensentation代写 文学论文代写 商科论文代写 艺术论文代写 人文代写 Case study代写 心理学论文代写 哲学论文代写 计算机论文代写



您必须登录才能发表评论。