ECON 257D2
Final Examination
Econ北美代考 Instruction: You may need the following information. z.05 = −1.6449 where, for any α ∈ (0, 1), we defifine zα as the α-th quantile…
Instruction: You may need the following information. z.05 = −1.6449 where, for any α ∈ (0, 1), we defifine zα as the α-th quantile of a standard normal distribution, i.e., if Z ∼ N(0, 1) then P(Z ≤ zα) = α. Econ北美代考
Problem 1: [5 points] Of a random sample of 172 elementary school educators, 118 said that parental support was the most important source of a child’s success. Test the hypothesis that parental support is the most important source of a child’s success for at least 75% of elementary school educators against the alternative that the population percentage is less than 75%. Use α = .05.
Problem 2: [15 points] Each day, a fast-food chain tests that the average weight of its twopounders is at least 32 ounces. The alternative hypothesis is that the average weight is less than 32 ounces, indicating that new processing procedures are needed. The weights of two-pounders can be assumed to be normally distributed, with a standard deviation of 3 ounces. The decision rule adopted is to reject the null hypothesis if the sample mean weight is less than 30.8 ounces.
(a) If random samples of n = 36 two-pounders are selected, what is the probability of a Type I error, using this decision rule?
(b) If random samples of n = 9 two-pounders are selected, what is the probability of a Type I error, using this decision rule? Explain why your answer diffffers from that in part (a).
(c) Suppose that the true mean weight is 31 ounces. If random samples of 36 two-pounders are selected, what is the probability of a Type II error, using this decision rule?
Problem 3: [10 points] Independent random samples of business managers and college economics faculty were asked to respond on a scale from 1 (strongly disagree) to 7 (strongly agree) to this statement: Grades in advanced economics are good indicators of students analytical skills. For a sample of 70 business managers, the mean response was 4.4 and the sample stan dard deviation was 1.3. For a sample of 106 economics faculty the mean response was 5.3 and the sample standard deviation was 1.4.
(a) Test, at the 5% level, the null hypothesis that the population mean response for business managers would be at most 4.0.
(b) Test, at the 5% level, the null hypothesis that the population means are equal against the alternative that the population mean response is higher for economics faculty than for business managers.
Problem 4: [35 points] Let the sample regression line be Econ北美代考

(c) Show that
SST = SSR + SSE.

(f) Using the result in part (e), show that the coeffiffifficient of determination is equal to the square of the sample correlation between X and y.
(g) Let b1 be the slope of the least squares regression of y on X, b∗1 be the slope of the least squares regression of X on y, and r be the sample correlation coeffiffifficient between X and y. Show that
b1b∗1 = r².
Problem 5: [35 points] Consider the following regression model: Econ北美代考
log(Wage) = β0 + β1 × Schooling + ϵ
where log(Wage) stands for hourly wage, Schooling for the years of schooling completed by the individual and can take values 0, 1, …, 20. Finally, ϵ is the error in the above regression model.
(a) Provide the condition under which E[log(Wage)|Schooling] = β0 + β1 × Schooling. Interpret the coeffiffifficients β0 and β1 from this relation.
In the rest of the problem (except in part(g)) we will assume that
E[log(Wage)|Schooling] = β0 + β1 × Schooling. (1)
Defifine 21 dummy variables S0, S1 . . . , S20 such that for j = 0, 1, . . . , 20 the random variable Sj = 1 if Schooling = j, and Sj = 0 otherwise.
(b) What is E[log(Wage)|S0, S1, . . . , S20]?
(c) Argue that there is no loss in generality in writing
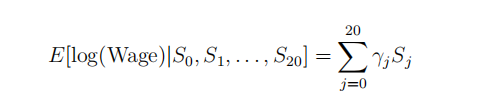
(2)
for some coeffiffifficients γ0, . . . , γ20.
(d) Argue that there is no loss in generality in writing
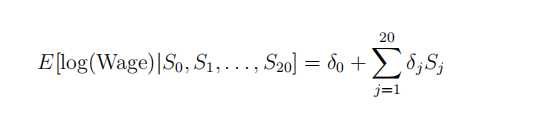 (3)
(3)
for some coeffiffifficients δ0, . . . , δ20. What is the relationship between the δj ’s in (3) and the γj ’s in (2)?
(e) Express the γj ’s in (2) in terms of β0 and β1 in (1).
(f) Express the δj ’s in (3) in terms of β0 and β1 in (1).
(g) Suppose that (1) is wrong. What is:
E[log(Wage)|Schooling = 12] − E[log(Wage)|Schooling = 5]?



