ECON 257D2
Final Exam
EconFinal exam代考 Roughly speaking, will the estimated coeffiffifficient of xt be (approximately) biased for β2? Why or why not?
Question 1: [5 + 5 + 5 = 15 points]
Suppose that the true regression model is:

(a) Roughly speaking, will the estimated coeffiffifficient of xt be (approximately) biased for β2? Why or why not?
(b) Suppose that you want to statistically test for this bias by looking at the covariance between xt and the residual from your (incorrect) regression that omits yt−1 as a regressor. Will such a test be meaningful? Why or why not?
(c) It is clear that unless β1 = 0 , the error in your incorrect model that omits yt−1 as a regressor will not independently distributed. Assuming that |β1| < 1, what will be the fifirst and second order autocovariance of the error in your incorrect model that omits yt−1 as a regressor?
Question 2: [5 + 5 = 10 points] EconFinal exam代考
(a) Provide an explanation for the difffference between the expressions for the standard errors (i.e., the ones with the square roots) in the expressions for the prediction interval and the confifidence interval in Equations 11.25 and 11.26 respectively on page 428 of the textbook.
(b) Consider a regression model:

Question 3: [5 + 5 + 5 + 5 = 20 points] EconFinal exam代考
Use the data from the worksheet “Question 3” in the fifile FinalExamData.xls. Consider the regression model:
y = β0 + β1X2 + β2X2 + β3X3 +
satisfying all the standard assumptions of multiple regression that we have maintained in this course. [Hint: The idea behind this question is similar to that of problem 12.54 in HW2.]
(a) Describe how you will estimate this model using least squares by imposing the restriction:
β0 = β1 + β2
such that you can also do a t-test for this restriction.
(b) Use the data for this question to perform the t-test for H0 : β0 = β1 + β2 and report your result.
(c) Describe how you will estimate this model using least squares by imposing the restriction:
β3 = β0 − β1 − β2
such that you can also do an F-test for this restriction.
(d) Use the data for this question to perform the F-test for H0 : β3 = β0 − β1 − β2 and report your result.
Question 4: [5 + 5 + 5 = 15 points] EconFinal exam代考
Suppose that you have two populations 1 and 2 and you have independent and identically distributed observations (y11, . . . , y1n1 ) and (y21, . . . , y2n2 ) drawn from populations 1 and 2 respectively. Assuming that these two populations are identical in all aspects expect possibly in their expectations, you set out to test H0 : µ1 = µ2 against H1 : µ1≠ µ2 where µ1 and µ2 are the expectations for populations 1 and 2 respectively.
(a) Defifine SST, SSW and SSG and describe how you will test H0 : µ1 = µ2 against H1 : µ1≠ µ2.
(b) Defifine y = (y1, . . . , yn1 , . . . , yn1+1, . . . , yn) = (y11, . . . , y1n1 , y21, . . . , y2n2 ), i.e., let the fifirst n1 observations in y be (y11, . . . , y1n1 ) and the last n2 observations in y be (y21, . . . , y2n2 ) where n = n1 + n2. Let X = (X1, . . . , Xn) be binary variables such that, for i = 1, . . . , n, we have Xi = 1 if the i-th observation comes from population 1 and Xi = 0 if the i-th observation comes from population 2. Describe how you will test H0 : µ1 = µ2 against H1 : µ1≠µ2 based on a regression of y on X.
(c) Comment on the relationship between the test statistics in your answers to (a) and (b).
Question 5: [4 + 4 + 4 + 4 = 16 points]
An agricultural experiment designed to assess difffferences in yields of corn for four difffferent varieties, using three difffferent fertilizers, produced the results (in bushels per acre) shown in the following table:
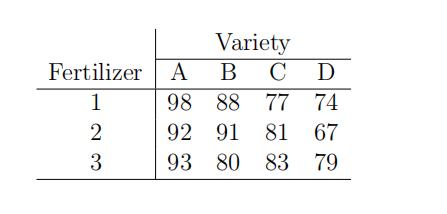
(a) Prepare the two-way analysis of variance table.
(b) Test the null hypothesis that the population mean yields are identical for all four varieties of corn.
(c) Test the null hypothesis that population mean yields are the same for all three brands of fertilizer.
(d) If the null hypothesis is rejected in (b) and/or (c) present a pairwise comparison among the varieties and/or brands to comparing them to their respective MSD’s.
Question 6: [5 + 5 = 10 points] EconFinal exam代考
(a) A random sample of 15 male students and an independent random sample of 15 female students were asked to write essays at the conclusion of a writing course. These essays were then ranked from 1 (best) to 30 (worst) by a professor. The following rankings resulted:
– Male: 26 24 15 4 8 30 11 25 19 5 13 19 10 28 8
– Female: 22 2 17 6 14 21 12 29 3 8 16 1 27 23 19
Test the null hypothesis that in the aggregate the two genders are equally ranked against a two-sided alternative.
(b) Explain the idea behind the use of contingency tables for testing association between two variables. Use your own words as if you are teaching someone, instead of just copying from the book or the notes.
Question 7: [4 + 4 + 6 = 14 points]
Use the data from the worksheet “Question 7” in the fifile FinalExamData.xls and answer the following questions.
(a) Run a regression of yt on yt−2 and comment on the coeffiffifficient of yt−2; in particular, check whether this coeffiffifficient is signifificantly difffferent from 0.
(b) Run a regression of yt on yt−1 and yt−2 and comment on the coeffiffifficient of yt−2; in particular, check whether this coeffiffifficient is signifificantly difffferent from 0.
(c) Is there any contradiction in the answers to (a) and (b)? Why or why not?



