FIN413 Quantitative Investment Analysis
Homework 4
fin代写 Note: This is an individual assignment. Don’t copy paste others’ reports, otherwise both you and other students who lend you…
Note: This is an individual assignment. Don’t copy paste others’ reports, otherwise both you and other students who lend you their copies will get zero scores! fin代写
- FormPortfolios by double independent sorting: Using the data from “project.csv” and “riskfactor.csv” from HW3, do independent double sorting At each the end of each month-t, sort all currently available stocks into five equal-numbered portfo- lios , based on their rankings in two different attributes independently: GP (Gross profitability) and log(BM) (log book-to market equity ratio). In other word, you generate two ranks for each stock independently, one based on its value of GP, and another based on its value of log(BM) (Note:Skip stocks at months with missing attributes.) Portfolio 5 contains stocks with the top 20% values of one attribute, while portfolio 1 contains stocks with bottom 20% values of the attribute.
Since we have two ranks associated with 2 attributes (GP, Log(BM)) for each stock, where each rank ranges from 1 to 5, we then take intersections of the two ranks. Conse- quently, you should get 5×5 = 25 portfolio, labelled as 11, 12,…15,21,22,…25,…,51,52,…,55. For instance, portfolio 11 includes stocks ranked bottom 20% in GP as well as in log(BM) simultaneously.
Compute the equally-weighted monthly excess return over [t, t + 1] for each portfolio, fin代写
that is, 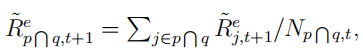 where
where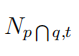 is the number of stocks in the portfolio labelled as pq (intersection of the set of stocks with rank p in GP and the set of stocks with rank q in log(BM)) at time-t and p, q ∈ {1, 2, …, 5}. Repeat above steps for every month to obtain the time series of monthly excess returns on the 25 portfolios (Note: Since the firm-level attribute are already lagged excess return data by one month, the sorting actually starts at 1963/6/30. The first return date should be 1963/7/31.).
is the number of stocks in the portfolio labelled as pq (intersection of the set of stocks with rank p in GP and the set of stocks with rank q in log(BM)) at time-t and p, q ∈ {1, 2, …, 5}. Repeat above steps for every month to obtain the time series of monthly excess returns on the 25 portfolios (Note: Since the firm-level attribute are already lagged excess return data by one month, the sorting actually starts at 1963/6/30. The first return date should be 1963/7/31.).
You should report 1. Means, standard deviations, and t-statistics of the mean, for the 25 portfolios excess returns and 10 long-short portfolios (given the rank of one attribute, buying portfolio 5 and short portfolio 1 for the other attribute) in the following table;
2. report their monthly CAPM alphas αp, t-statistics of αp and the regression R2s using the following time-series regression: fin代写
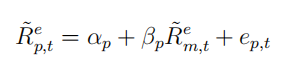
Describe your findings by covering the following questions: 1. How do the av- erage excess returns of the 25 portfolios vary with their rankings in the two attributes? Can you interpret these patterns? 2. Among the 10 long-short portfolios (5-1), which one can generate an average excess return significantly different from 0? 3. Which long-short portfolio can yield CAPM α significantly different from 0? 3. Which port- folio has the largest CAPM α? 4. Comparing to the results of single sorting by GP or by Log(BM) in your HW3, does the double-sorting enhance or reduce the CAPM alpha of the long-short portfolios?
| GP Rank (row) | Log(BM) (col) | 1 | 2 | 3 | 4 | 5 | 5-1 (Log(BM)) |
| 1 | Mean SD
t-stat CAPM α CAPM α t-stat R2 |
||||||
| 2 | Mean SD
t-stat CAPM α CAPM α t-stat R2 |
||||||
| 3 | Mean SD
t-stat CAPM α CAPM α t-stat R2 |
||||||
| 4 | Mean SD
t-stat CAPM α CAPM α t-stat R2 |
||||||
| 5 | Mean SD
t-stat CAPM α CAPM α t-stat R2 |
||||||
| 5-1 (GP) | Mean SD
t-stat CAPM α CAPM α t-stat R2 |
2.Using the data from “project.csv” and “riskfactor.csv” from HW3, implement amomentum strategy. A momentum strategy is to long stocks with highest past returns (past winners) over a certain period and short stocks with lowest past returns (past losers) over the same period. It has two dimensions, a formation period f and a holding period h. The goal is to help you implement a monthly momentum strategy with f = h = 6 fin代写
- f = 6 means the formation period is 6 months, meaning that momentum is measured by past 6 month cumulative excess return. You long stocks with highest past 6 month returns and short stocks with lowest 6 month Accordingly, you should compute the past 6 month cumulative excess return on each stock i at the beginning of each time-t,
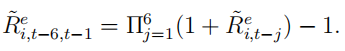
- h= 6 means that the holding period is also 6 That is, you hold your stocks (in either long side or short side) for 6 months.
- Supposeyour sort stocks into 5 equal-numbered Because of the 6- month holding period, the month-t + 1 long side portfolio consists of stocks with ranks in 1. top 20% R˜ei,t−5,t 2.top20% R˜ei,t−6,t−1 3.top20% R˜ei,t−7,t−2 4.top20%R˜ei,t−8,t−3 5.top20% R˜ei,t−9,t−4 6.top20% R˜ei,t−10,t−5. The excess return on the month-t + 1 long side portfolio is computed as the simple average of the 6 sub portfolios. Note if any of past 6 month excess returns are missing, drop this stock for that sub portfolio. fin代写
-
Similarly,the month-t + 1 short side portfolio consists of stocks with ranks in bottom 20% R˜ei,t−5,t 2.bottom20% R˜ei,t−6,t−1 3.bottom20% R˜ei,t−7,t−2 4.bottom 20% R˜ei,t−8,t−3 5.bottom 20% R˜ei,t−9,t−4 6.bottom 20% R˜ei,t−10,t−5.
- The excess return on the month-t + 1 short side portfolio is computed as the simple average of the 6 sub portfolios. Again, drop stocks for a sub portfolio if that past 6-month return is missing.
- Theexcess return from the momentum strategy is the difference between the return on the long-leg portfolio and the return on the short-leg
- Because of the 6-month formation period, the excess return on this momentum strategy starts from 1964 and ends on Jan 2015. Please following the procedure above and report 1. the time series of excess returns on the momentum strategy; 2. mean, standard deviation, t-stat of mean, Sharpe ratio, CAPM α, t-stat of CAPM α, and CAPM regression R2 of the excess return from this strategy,
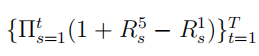 ; 3. plot the cumulative excess return on this trading strategy; 4. Expalin your findings.
; 3. plot the cumulative excess return on this trading strategy; 4. Expalin your findings.
- Using the file “performance.csv” from HW4, compute the following performance mea-sures for two hybrid (equity+bond) mutual funds. In this file, t is measured in month. Column 2 is the monthly return on “华夏成长” and column 3 is the monthly return on “南方稳健成长”. Column 4 is the market return Rm,t (中证A指全收益). The last column is the monthly risk-free rate, measured by one-month T-bill rate.

Denote monthly market excess return as Re = Rm,t − r and monthly portfolio excess return as Re = Rp,t − r where p = 1, 2. Complete the following questions: fin代写
- Annualized average excess returns of the two funds and the market: Mean(Re )∗12, k = 1, 2, m
- Annualized standard deviations of excess return of the two funds and the market: Std(Re ) ∗√12, k = 1, 2, m
- Annualized Sharpe ratios of the two funds and the market:
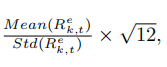 ,k=1,2,m
,k=1,2,m - Annualized CAPM alpha and t-stats:
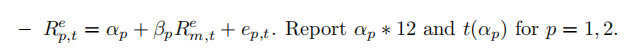
- CAPM beta βp and annualized systematic volatility βp ∗ Std(Re) ∗ √12 for p = 1, 2.
- AnnualizedTreynor ratios for the two funds:
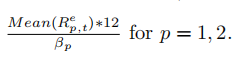
- Annualizedidiosyncratic volatility: σ(ep,t) ∗ √12, where ep,t is the residual of the time series regression, for p = 1, 2.
- R2of the CAPM time series regression for the two funds.
- Informationratio (relative to the CAPM): σ(ep,t) , for p = 1, 2.
- Maximal Drawdown(not annualized) of the cumulative fund returns for the two funds.
[Hint]: you need to first compute the cumulative wealth from investing in a fund. For instance, at time-t, the cumulative wealth of investing in a fund is Wt ≡ Πt (1 + Rp,j) and W0 ≡ 1.
- Maximal RecoveryPeriod (not annualized) of the cumulative fund returns, for the two funds.
[Hint]: Again you need to compute the cumulative wealth from investing in a fund.
- Markettiming regression test:
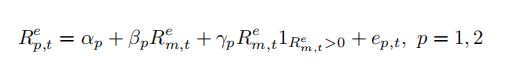
Report the estimates of γp of the two funds and their t-statistics. Which fund has market timing ability?
- Suppose you plan to invest all of your wealth exclusively in one of the two Which one will you choose? Explain the reason in detail.
- Suppose you plan to invest your wealth in several different funds to form a well-diversified You invest only a fraction of your total wealth in one of the two funds and you cannot short these funds. Which one will you choose? Explain the reason in detail.
- Suppose you want to build an enhanced-index portfolio. You overall portfolio is a mixture ofthe market index and one of the two mutual funds. Suppose you can short these funds freely, which one will you choose? What is the maximally attainable Sharpe ratio of your optimal portfolio?



