Final Exam: AME 509, Applied Elasticity
Final Exam代做 Lots and lots of tensor and index notation; 10 points. Let e1,2,3 be a right-hand orthonormal frame. a = aiei , b = biei , A = Aijei ⊗ ej , B = Bijei ⊗ ej
(1) Lots and lots of tensor and index notation; 10 points. Let e1,2,3 be a right-hand orthonormal frame. Let Final Exam代做
a = aiei , b = biei , A = Aijei ⊗ ej , B = Bijei ⊗ ej
in index notation. Consider the vector function
v(a, b, A, B) = Tr(a ⊗ b)b + |b| 2 a + Tr(ATB)(a − b) + Aa + Bb.
(i) (2 points.) Let v(a, b, A, B) = vi(a, b, A, B)ei where vi(·), i = 1, 2, 3, denote the component of v(·) in the given basis. Provide an explicit formula for these three components in terms of the components of a, b, A, B. Hint. In other words, write the vector function v(a, b, A, B) in index notation.
(ii) (2 points.) For v ≡ v(a, b, A, B) defifined above, compute the derivative Final Exam代做

as depicted in the fifigure. It is then subjected to the deformation Final Exam代做
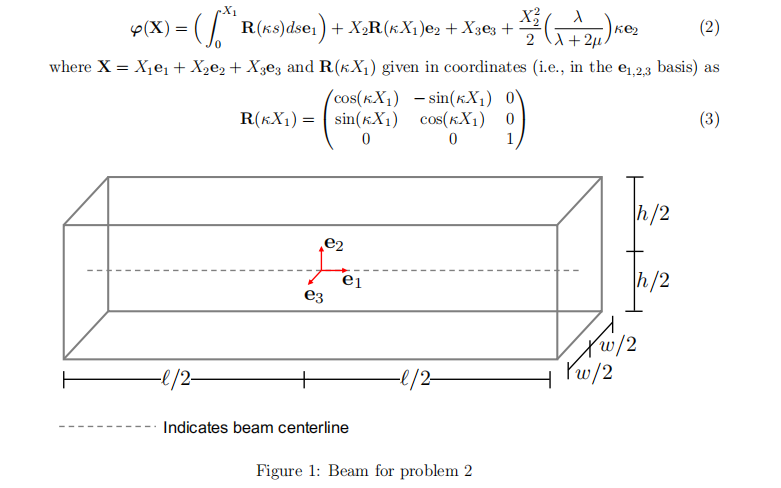
(a) (2.5 points.) Determine the smallest positive value of κ (call it κ ? ) for which the endpoints of the centerline of the beam come into contact, i.e.,
(b) (0.5 points.) Suppose κ = κ ? as determined above. Sketch the deformation of the centerline of the beam, i.e., the deformation ϕ(X1e1), X1 ∈ (−`/2, `/2).
(c) (0.5 points.) Suppose instead that κ = κ ? /2. Sketch the deformation of the centerline of the beam in this case.
(d) (0.5 points.) What does the parameter κ describing in the deformation? Final Exam代做
(e) (3.5 points.) Now assuming κ is completely general, i.e., is not constrained as above, compute the deformation gradient F(X) = ∇ϕ(X) of the deformation in Eq. (2). Hint. When X2 = 0, you should fifind that your solution satisfifies F(X1e1 + X3e3) = R(κX1).
(f) (1 points.) Now let’s assume 0 < κ 1. Linearize your result for the deformation gradient above by computing the linearized deformation gradient Flin(X) such that
F(X) = Flin(X) + O(κ ² ). (5)
Here O(κ 2 ) includes terms that are proportional to κ 2 , κ3 , . . . , etc.
(g) (0.5 points.) Let ∇Ulin(X) = Flin(X) − I. Compute the linearized strain tensor for this displacement lin(X) =½(∇Ulin(X) + ∇Ulin(X) T ).
(h) (0.5 points.) Assume that, when 0 < κ 1, it is justifified the to consider the beam as linear elastic and isotropic as a function of the strain lin(X). In this setting, determine the Cauchy stress in the beam.
(i) (0.5 points.) Show that, when there are no body forces, the beam is in static equilibrium under the linearization above.
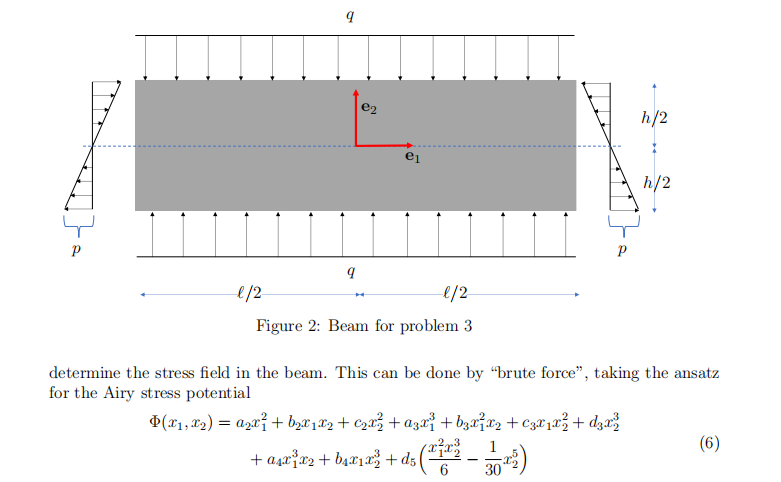
(3) Another beam problem; 10 points + 2 bonus points. Consider the beam under uniform loading profifiles of magnitude q ≥ 0 on its top and bottom surface and a linear load profifile of maximum magnitude p ≥ 0 on its sides, as depicted in Fig. 2. The goal of this problem is to Final Exam代做
Though hint: If you can think of a simpler way to solve this problem, you are absolutely free to do so.
(a) (3 points.) Formulate the appropriate boundary conditions for the beam under the loading described in Fig. 2.
(b) (7 points.) Determine the stress fifield in the beam.
(c) (2 bonus points.) Can you describe the relationship between the beam in Problem 2 and the beam in Problem 3. Full credit for a quantitative description (Hint: Maybe there is a setting in which κ and p can be directly related to each other?); half credit for a qualitative description.
(4) (1D bar revisited; 5 points.) Recall from the fifirst lecture that a linear elastic 1D bar from Fig. 3 satisfifies Final Exam代做
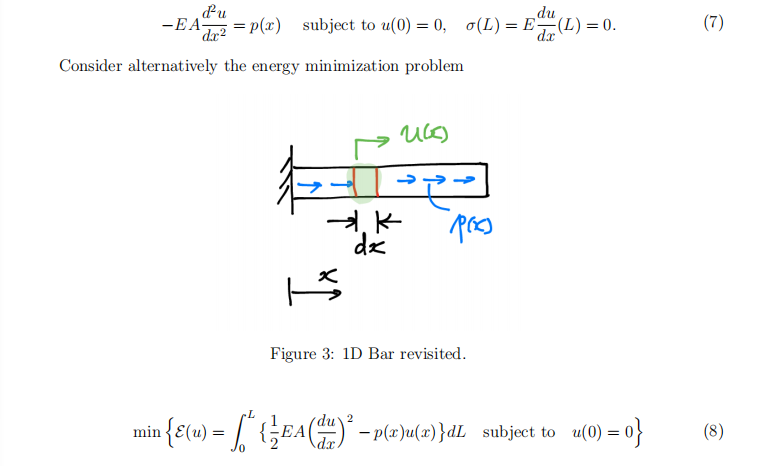
Use the calculus of variation to show that a minimizer u ? (x) to Eq. (8) satisfifies the equilibrium equation in (7).



