Math 4446
Project 1
math作业代写 Instructions: Scan your written solution and upload it to Canvas. Your written solution does not have to be typed on a computer…
Instructions: Scan your written solution and upload it to Canvas. Your written solution does not have to be typed on a computer but it has to be clear, legible and in a single fifile (preferably PDF). If you are uploading a MATLAB fifile or a image fifile with your solution, put everything in a ZIP fifile.
Problem I: (Defeating the Runge phenomenon using Chebychev nodes) math作业代写
You have seen that in the case of 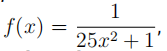 , the interpolating polynomial pn does not converge uniformly to f on [−1, 1] when using equidistant nodes. First, let us discuss why this happened:
, the interpolating polynomial pn does not converge uniformly to f on [−1, 1] when using equidistant nodes. First, let us discuss why this happened:
- Recall that
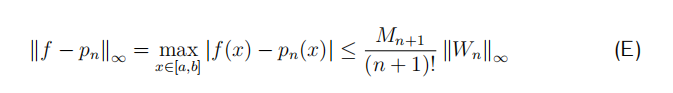
where
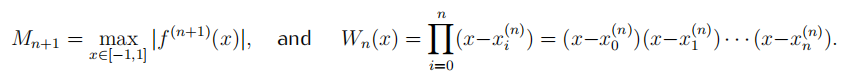
To understand why Runge chose this specifific function, do the following: math作业代写
(a) For n = 5, 8, 10, compute and plot |f(n+1)(x)| on [−1, 1].
(b) Estimate graphically (you do not have to be accurate) Mn+1 for the previous three values of n.
(c) Let {x(in)} be the equidistant nodes described in the fifirst homework. Plot![]() for n = 5, 8, 10 and estimate graphically
for n = 5, 8, 10 and estimate graphically ![]()
(d) Does the right hand side in inequality (E) seem to go to zero as n → ∞?
The question (a) can be a bit diffiffifficult to implement if you are computing the derivatives by hand. Here’s a simple way to plot it
1 clear 2 3 n =5; %n is an integer bigger than or equal to 1 4 5 syms f ( x ) 6 f ( x ) = 1/(25* x ^2+1) ; 7 df = diff (f ,x , n +1) ; %the (n+1) -th derivative of f 8 ezplot ( df ,[ -1 ,1]) % the plot 9 ylim ([ - inf , inf ]) % to make sure that is the graph is fully visible .
You can change the value of n in the third line. math作业代写
- Now, you’ve noticed that 丨丨Wnll丨丨 ∞ is not decaying fast enough. Fortunately, there is a better choice of nodes in [−1, 1] that makes it decay faster, these nodes are called Chebyshev nodes and they are given by
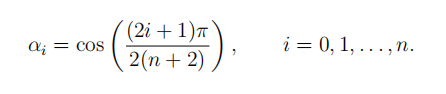

Figure 1: Pafnuty Chebyshev 1821-1894

This means that Chebyshev nodes are the nodes that give us the smallest value of 丨丨Wnll丨丨 ∞ . If you want to see a proof, let me know.
Redo 1.c with these Chebyshev nodes, do you see an improvement?
- Interpolate f at the Chebyshev nodes with n = 5, 10, 20 and plot the results (plot f and pn in the same fifigure, you would have three graphs, see lesson 4 for more details).
- Did the Runge phenomenon disappear?
Problem II: (Interpolating expensive functions) There a function next to this PDF called expensive f.m, download it. math作业代写
This function is expensive in the sense that computing a single evaluation takes a long time (it takes one or two seconds on my laptop). In the remainder of this problem, I will be using f(x) for expensive f(x)
- Compute f(0), f(.5) and f(1), how long did each evaluation take?
To find the time it took MATLAB to evaluate f, you could use:
tic; expensive_f(0) toc;
toc prints out the time it took the processor to evaluate all the commands between tic and toc. math作业代写
- Plot f on the interval [0, 1] using 500 plot points, notice that this is not a vectorized function, so you need to evaluate it at every plot point separately. While your code is running, give an educated guess on how long do you think that it would take MATLAB to fifinish the plot.
- Save the previous plot.
- Find a linear function T that maps the interval [−1, 1] to [0, 1].
- Use T to map the Chebyshev nodes from [−1, 1] to [0, 1].
- How many Chebyshev nodes should you use if you want to plot an interpolation of f using 500 plot points and not exceeding 30 seconds in processing time? Save the plot.
- Compare the two plots (you can plot |f(x) − pn(x)|, what do you conclude?
Note: This function came to me from a friend, it appeared in equation (55) in this research paper: https://ieeexplore.ieee.org/document/7892914 , I do not claim to know the full story behind it but I would be more than happy to ask them for more details if you are interested.

更多代写:machine learning代写 多邻国代考 SQL作业代写 会计作业代写 economic代写 cs代码代写


