MATH序列代考 MATH 153 E代考 quiz代考

MATH 153 E

MATH序列代考 The exam is out of 150 points. Partial credits will be given. You should give reasons or show your work. 

• The exam is out of 150 points.

• Partial credits will be given.

• You should give reasons or show your work.

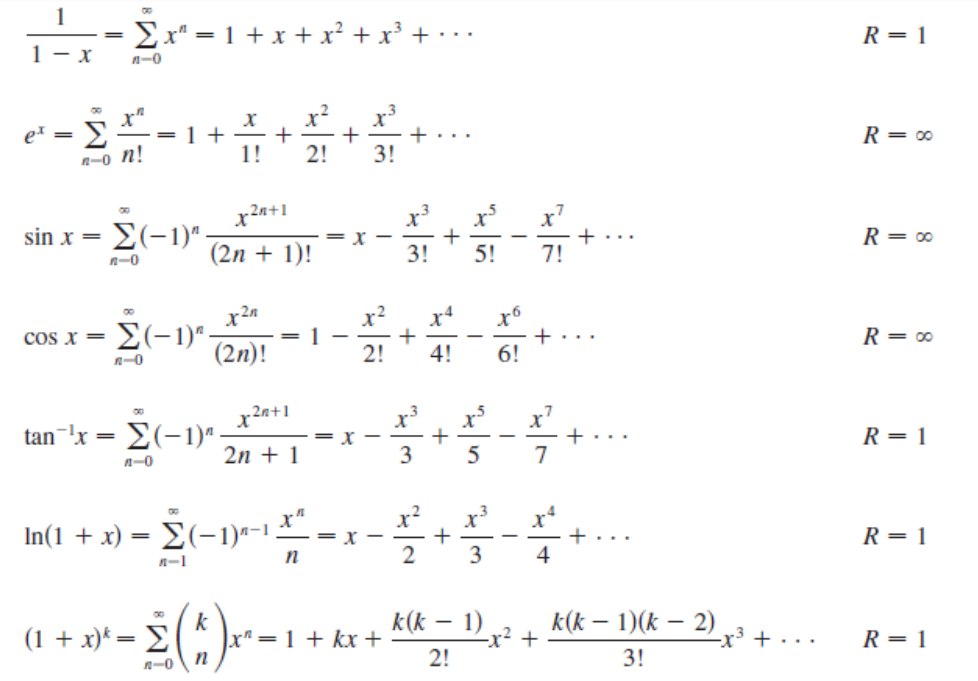
1. (4p.) Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues:

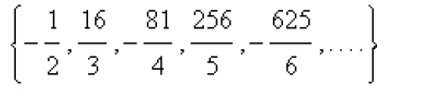
2. (12p.) Determine whether the sequence converges or diverges. If it converges, find the limit. MATH序列代考

3. (12p.) Determine whether the series is convergent or divergent. If it is convergent, find its sum.

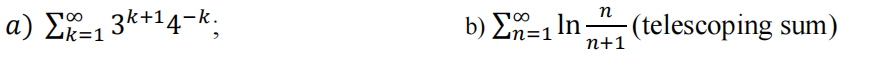
4. (10p.) Use the binomial series to expand the function as a power series. State the radius of convergence: (1+ x)3/4 .

5. (32p.) Test the series for convergence or divergence. MATH序列代考

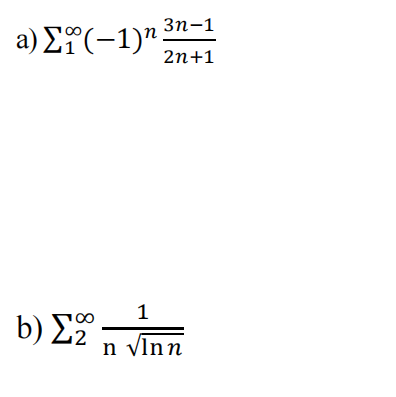
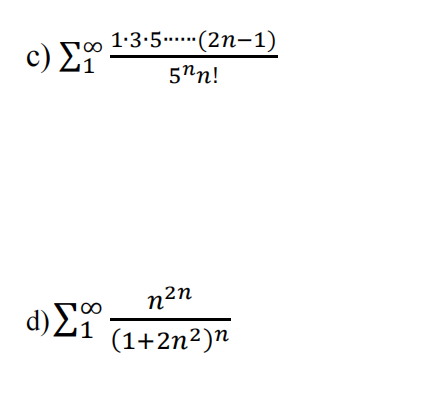
6. (8p.) Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent.

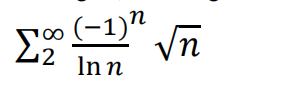
7. (8p.) Find the radius of convergence and interval of convergence of the series: MATH序列代考

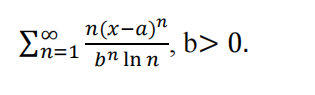
8. (10p.) Express the function as the sum of a power series by first using partial fractions. Find the radius of convergence. f(x) =(2x – 4)/(x2 – 4x + 3).

9. (8p.) Show that 0.9999…= 1
10. (10p.) Find the Maclaurin series for f (x) using the definition of a Maclaurin series. Also find the associated radius of convergence: f(x) = 10x

11. (12p.) Find the Taylor series for f (x) centered at a = π/6 using the definition of a Taylor series ???? ???? ?ℎ? ?????????? ?????? ?? ???????????: ?(?) = ????.

12. (8p.) Use series to evaluate the limit. MATH序列代考

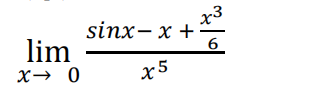
13. (8p.) Find the sum of the series.

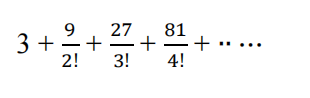
14. (8p.) Evaluate the indefinite integral as a power series. What is the radius of convergence?

∫ ?² ln(1 + ?) ??