Handover with Network Slicing in 5G Networks
Department of Computer Engineering, NETLAB
NETLAB代写 Abstract—The wide variety of new opportunities offered by 5G, together with the very large number of mobile devices, imposes signifificant…
Abstract—The wide variety of new opportunities offered by 5G, together with the very large number of mobile devices, imposes signifificant challenges in network operation. Network slicing provides effificient operation of the network under these conditions by separating the slices. However, scalable and flflexible approaches are required to allow for the dynamic load of the network. Network slicing is the concept of having multiple isolated virtual networks on top of the same physical infrastructure. As the result of flfluctuations (due to mobility or varying offered traffific), a UE may be subject to handover between cells.
The selection of the UE and the corresponding service base station (BS) may hamper utilization if the UE undergoing handover cannot be offered the same slice capacities by the destination BS. In this paper, we propose handover to increase the utilization of the radio resources by selecting the UEs that undergo handover according to the required services for each slice and the availability of those slices at the destination BS. We develop an optimization problem to optimize the radio resources and propose three heuristics to reach similar results in considerably low computing times. We simulate the results of the algorithms and show that our heuristics can present solutions close to the optimal within a short time frame.
Index Terms—5G networks, Network Slicing, Handover, Optimization
I.INTRODUCTION NETLAB代写
Dividing the network to provide various services is one of the striking aims of 5G [1]. To meet this target, 5G introduces network slicing, which utilizes one physical infrastructure for various virtual networks [2]. With the use of different virtual networks, various communications can be supported (e.g., IoT, mobile devices, vehicle communications, and robots) on the same physical infrastructure.
For different slices that use the same physical infrastructure, latency, throughput, and bandwidth can be assigned in various ways with different resource allocation methods. Radio resource allocation for the slices can be performed by resizing the slice bandwidths [3], [4] or by using handover algorithms [5]. Slice assignments for the users can be done in different ways. [6] states two methods for the slice assignments. In the fifirst method, user equipments (UE) are responsible for the slice selection. On the other hand, second method suggests that the core network is responsible for the slice selection and makes decisions according to the UE’s service request. Furthermore, a UE can get service from multiple slices concurrently by using one access and mobility management function [7].
Slice isolation is also considered for network slices and different methods are suggested to maintain isolation. One of the radio access network (RAN) isolation methods is to use scheduling to ensure the interception between slices is eliminated. Second method is to assign dedicated spectrum for each slice [1], [7]. NETLAB代写
Some of the recent studies on network slicing can be listed as follows: In [8], maximization of the throughput is targeted for the slice selection problem with handover. A genetic based heuristic algorithm is proposed to solve the problem. Greedy algorithm, random assignment algorithm and genetic algorithm are compared in terms of performance. The benefifit of the genetic algorithm for handover success rate and throughput can be observed when the number of users in the network are not sparse.
In [9], network slice admission problem is studied. Upcoming slice demands of the users are predicted with the Holt-Winter method that is used for time-series forecasting. Then, according to these predictions, a heuristic algorithm is proposed for the slice allocation problem. It is shown that with the forecasting scheme, higher network utilization can be achieved while the slice demands and network capacity increases.
In [10], slice allocation problem is studied with user centric perspective. The problem objective is constructed as the weighted average of different user demands such as latency, user priority, and user/slice bandwidth. In order to solve this problem, inter-slice handover mechanism is proposed. When there is a network congestion, inter-slice handover is used to reduce the load by blocking the UEs from their initial slice candidate. It is shown that, in the case of congestion, the proposed solution is effective in solving the proposed problem.
In [11], handover problem is studied with reinforcement learning methods. The authors assume that each slice is provided by different subset of BSs. They defifine the handover costs, then establish a problem with an objective of minimizing long-term handover costs. Moreover, in [12] and [13] reinforcement learning is used for network slice resource management. In addition, in [14], deep neural networks are adopted for the forecasting of slice type from the traffific patterns. Then, by using the output of the neural network, a new device is assigned to the proper slice. Studies that are presented in this paragraph illustrate how machine learning can be useful in handling the problems of network slicing. NETLAB代写
The aim of this paper is fifirst to defifine a joint handover/slice allocation problem. Then, we propose three heuristics to decrease the algorithm execution time. We show that even though proposed heuristics do not provide the optimal solution, close-to-optimal solutions are found within a very short time frame. The contributions of this paper can be summarized as:
- An optimization problem that targets to maximize the total number of slice connections in 5G networks is defifined. The fundamental distinction of the defifined problem is that the problem considers users’ slice demands, required data rates for each slice usage, and the existing capacity of the slices in all BSs. As a result, we fifind a good assignment of the users to the BSs and increase the overall slice utilization.
- For the defifined nonlinear optimization problem, a linearization method is employed such that the resulting linear problem can be solved within a shorter time compared to the original problem.
-
In order to solve the proposed problem, three heuristic methods are developed. One of the heuristics focuses on assigning the users to the most idle BSs to increase their slice usages. The remaining two algorithms employ different handover methods to improve the RAN utilization and the number of total slice connections.
- We solve the defifined problem with the well-known optimization toolbox called Gurobi [15] and compare the solutions with the proposed heuristics. Success of the algorithms is illustrated with simulations. Overall, we demonstrate that the Intelligent Handover Algorithm is a good method to solve our defifined problem. NETLAB代写
The remaining parts of this study can be summarized as follows. In Section II, the mathematical preliminaries and the 5G system model are introduced fifirst. Then, the joint handover/slice allocation problem is formulated as an optimization problem. In addition, employed linearization approach for our problem is shown. In Section III, details of the heuristic algorithms are discussed. The performance of the proposed algorithms along with the Gurobi toolbox are illustrated via simulation results in Section IV. Finally, concluding remarks are discussed in Section V.
II.A JOINT HANDOVER/SLICE ALLOCATION PROBLEM FOR 5G NETWORKS
For 5G networks, we study a network that contains many BSs, which support the same set of slices. Slice capacities in this network are fifixed and slices can support a limited number of users. Concurrent slice usage for the UEs in the network is supported. Required data rate on the same slice is assumed to be fifixed for all UEs. Fixed capacity of the slices may result in accepting fewer slice service requests. In order to addressthis issue, an optimization problem is defifined to improve RAN resource utilization for the slices of 5G networks.
A.Network Model NETLAB代写
In the network model, it is assumed that UEs are represented by k (k 2 K = {1, 2,…,K }). The BSs in the network are denoted by n (n 2 N = {1, 2,…,N}). Consider each slice is denoted by s and the number of slices in the network is S. The set of slices is defifined as S = {1, 2,…,S}.
Coverage area information of UE k by BSn is denoted by the binary variable cnk and is defifined as


UEs can only be connected to one BS (5b) that they are covered by (5c). If UE k is connected to a BS and demands to use slice s, then it can be provided with slice s (5d). The capacity of the slices are not violated by enforcing the constraint (5e). Finally, (5f) and (5g) restrict the decision variables to be binary.
The problem defifined in (5) is a nonconvex Mixed Integer Quadratically Constraint Programming (MIQCP), where the quadratic, nonconvex constraint comes from (5e). The analytical solution for these problems does not exist, whereas the numerical solutions are considered as NP-hard [16]. A broad survey given in [17] on nonconvex Mixed Integer Nonlinear Programming (MINLP), of which MIQCP is a subset, outlines the existing methods for solving nonconvex MINLP types of problems. In this paper, we employ the method of Conversion to Mixed Integer Linear Programming (MILP).
C.Linearization of Quadratic Constraints NETLAB代写
Quadratic constraints can be converted into a set of linear inequalities [18]. In order to linearize the quadratic constraint in (5e), we introduce a new variable such that mn k,s = xn k pk,s, and new constraints. The problem is redefifined as:
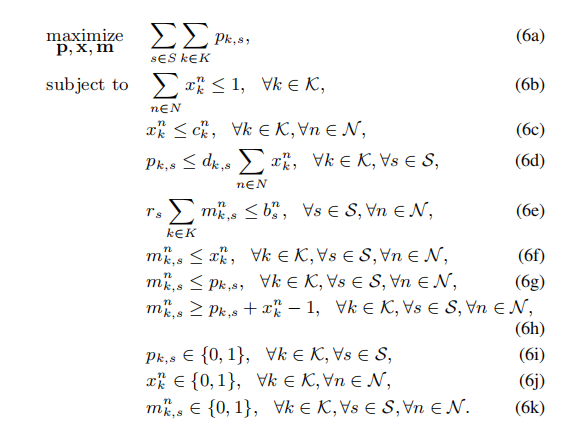
We use the MILP defifined in (6) in our simulations.
III. HEURISTIC ALGORITHMS FOR JOINT HANDOVER/SLICE ALLOCATION (JHSA) PROBLEM
In this section, we propose three heuristic algorithms for the problem described in Section II. The proposed heuristics aim to fifind solutions to the defifined problem in a shorter time frame while adhering to the same constraints.
A.Simple Algorithm NETLAB代写
The proposed Simple Algorithm provides an effificient slice assignment process for the incoming UEs. This algorithm assigns the UEs to the BSs with relatively lower load. It targets to distribute the UEs as evenly as possible in the network. Slice utilization and used slice capacity are calculated with every incoming user. The load of slice s in BS n can be calculated as
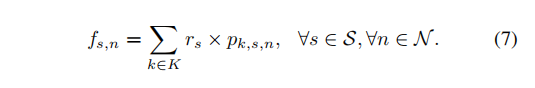
Utilization of each slice can be found as follows:
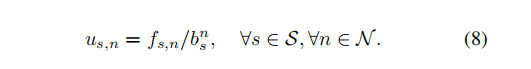
BS and slice assignments are performed until the network capacity is reached in the entire network. When (9) is met, the admission of UE to the BS is performed and the slices are provided. Admission is possible when at least one of the requested slices can be provided.
![]()
B.Greedy Handover Algorithm
We propose a heuristic algorithm that simultaneously performs the handover of the UEs and their slice assignments. While the number of users increases, without exceeding the capacity limits for each slice, the algorithm performs handovers of the possible UEs to provide the maximum service for network slices that are demanded by the UEs. If a UE is in the intersection area of its current base station and neighboring station, and the load of the slices it demands is lower in the neighboring station, handover can be performed. In summary, this algorithm ensures that the resources of the network are effificiently distributed amongst network users. Thus, the overall utilization is maximized. We only focus on handover of the UEs when there is a connection request coming from a UE within the coverage area of only one BS.
C.Intelligent Handover Algorithm NETLAB代写
We propose Intelligent Handover Algorithm that introduces an intelligent decision mechanism for the handover of users to the neighboring stations. Simple Algorithm lacks flflexibility of rearranging UE-slice assignments to increase the available capacity when the load increases for some of the BSs in the network. Greedy Handover Algorithm does not consider continuity of the connections. Therefore, after handover, the slices that UEs use on the source BS, may not be provided on the target BS.
The implementation of Intelligent Handover Algorithm is given in Algorithm 1, where the time complexity of the algorithm is O(K2·N ·S). In order to solve the communication break problem seen in the Greedy Handover Algorithm, we implement additional controls for the handover decision. We use sk,cont vector, which is calculated as
sk,cont = ˆpk − pk. (10)
We check if the slices that are currently in use will be provided after handover. If that is the case, handover is performed.
IV.SIMULATION RESULTS
Simulations are performed under two scenarios. Firstly, in IV-A, we consider a scenario where the user locations are generated by a uniform random distribution throughout the entire network. Secondly, we examine a scenario where the density of the UEs increase when we move towards the BSs located on central areas.
Algorithm 1 Intelligent Handover Algorithm with Network Slicing NETLAB代写
Input: N, S, list of cnk , list of dk,s, list of bns , list of rs
Output: algorithm exec time, total num of pk,s, avg utilization of BSs and slices


A.Uniformly Distributed Random Placement Scenario
Network parameters in this scenario are taken as defifined in Table I and BSs are located as shown in Fig. 1. UE locations
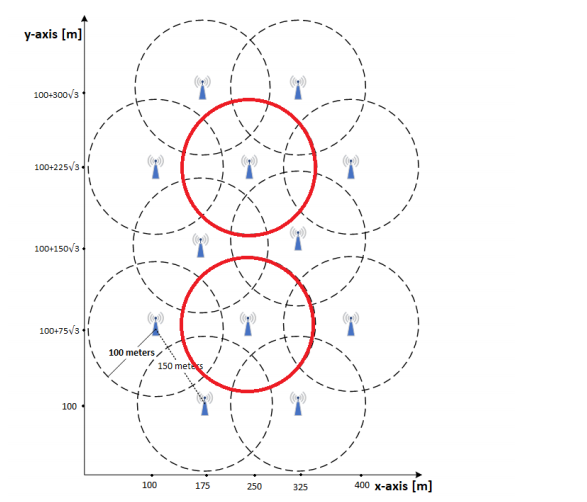
Fig. 1. Base Station Locations
TABLE I
SIMULATION PARAMETERS
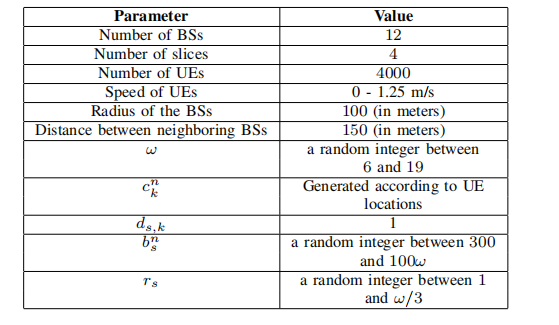
are generated by using a uniform random distribution within the boundaries of the network and movement of the UEs is simulated as Brownian motion. Simulation continues for 300 seconds and all algorithms are run every two seconds. We compare the performance of the proposed heuristics and Gurobi solution according to the following metrics: algorithm execution time and overall slice utilization in the network. In addition, we have shown the optimality gap of Gurobi solution when a time limit is set for Gurobi.
As can be seen in Fig. 2, Gurobi execution time to fifind the optimal solution is very high and flfluctuates signifificantly. Thus, we also added a time limit for Gurobi and the proposed algorithms for under two seconds. NETLAB代写
As illustrated in Fig. 3, when two seconds time limit is applied for Gurobi, total slice utilization it can reach is lower than the utilization that the proposed heuristics can provide. If no time limit is applied, Gurobi reaches the best solution. Yet, the difference between Gurobi and the proposed heuristics is around 1%.
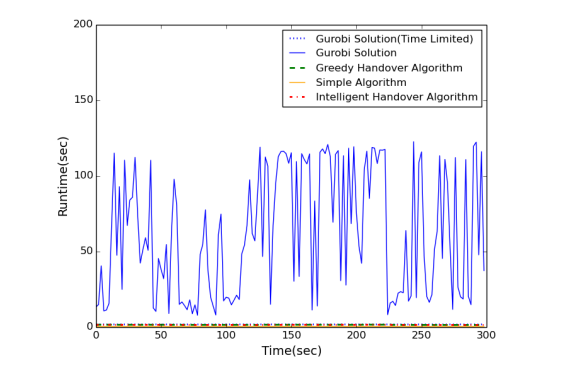
Fig. 2. Run times of the algorithms
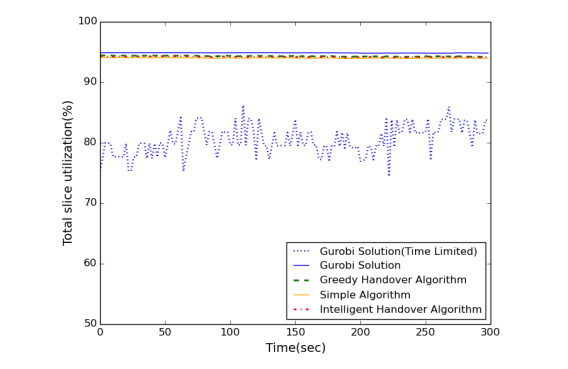
Fig. 3. Overall slice utilization
Fig. 4 shows the optimality gap for Gurobi time limited solution. Gurobi is unable to reach optimal solution when two seconds limit is applied to solve the defifined problem. The closest it can get to the optimal solution flfluctuates between 20% and 40%. NETLAB代写
Overall, the proposed heuristics are able to provide good results within a shorter time frame, and the solutions are better than Gurobi when time limit under two seconds is applied.
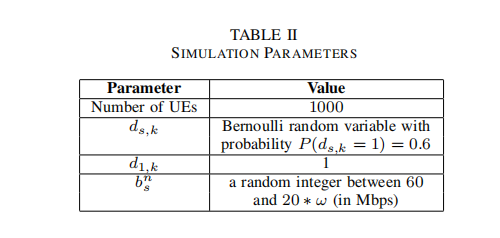
B.Crowded Center Scenario
Some of the network parameters in this scenario are changed as in Table II, remaining parameters are taken as in Table I. BSs are located as shown in Fig. 1 and the density of the
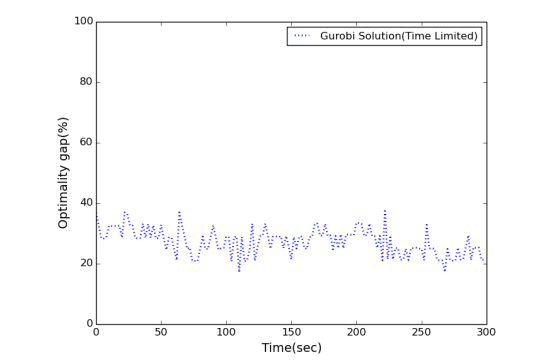
Fig. 4. Optimality Gap
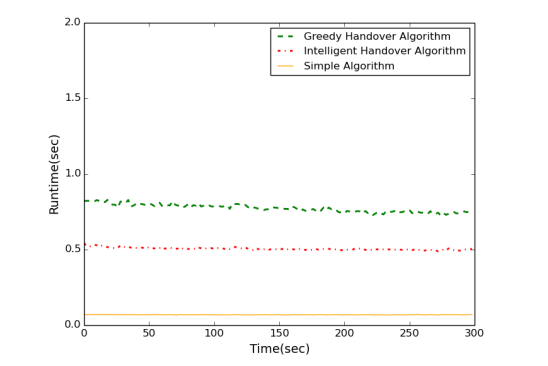
Fig. 5. Run times of the algorithms
users is taken as double in the center BSs (circled in red) compared to its surrounding BSs. Movement of the UEs is simulated as Brownian motion. Simulation is continued for 300 seconds and all algorithms are run every two seconds. We compare the performance of the proposed heuristics according to the following metrics: algorithm execution time, overall slice utilization in the network, total number of handovers and total number of dropped slice connections.
Fig. 5 shows that all algorithms fifind solutions less than one second: Simple Algorithm performs the best whereas Greedy Algorithm performs the worst. However, according to the Fig.6, this situation is vice versa. NETLAB代写
Our aim is to increase the overall slice utilization, while having low runtime, less number of handovers and less number of dropped slice connections. According to Fig. 7 and 8, Simple Algorithm causes the lowest number of handovers and dropped slice connections. However, Simple Algorithm is ineffificient for increasing the overall slice utilization. Intelligent Algorithm is good at increasing the overall slice utilization as well as keeping the handover rate and dropped connection number low compared to other two heuristics.
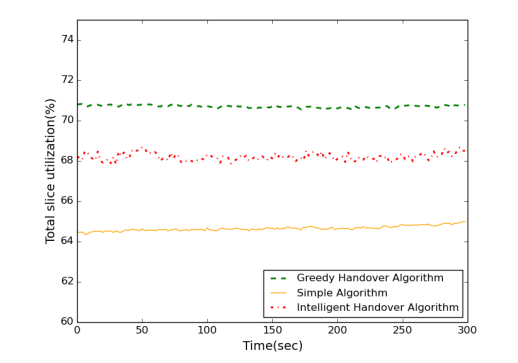
Fig. 6. Overall slice utilization
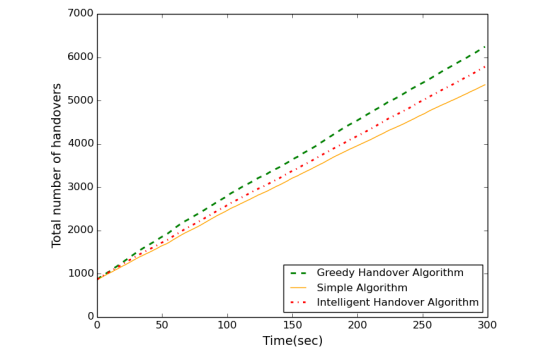
Fig. 7. Total number of handovers
V.CONCLUSION
In this study, an optimization problem is defifined to maximize the utilization of radio resources of network slices. For the defifined problem, a solver is used for the simulations. Three heuristic algorithms are proposed to reach similar results
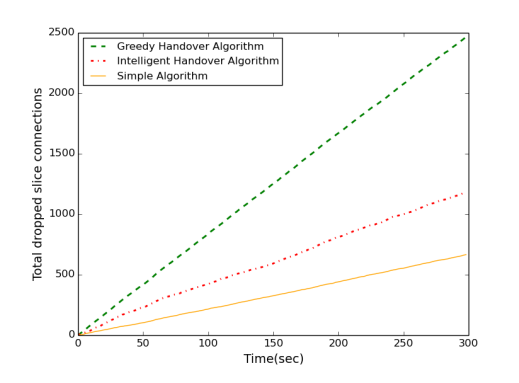
Fig. 8. Total number of dropped slice connections as the solver, but with considerably lower computing times. The simulations verify that the proposed Intelligent Handover Algorithm is a promising approach, offering comparable performance to that offered by the solver while providing scalability.
ACKNOWLEDGMENT
This work is partially supported by TUBITAK under project number 119C055 and by the Turkish Directorate of Strategy and Budget under the TAM Project number 2007K12-873.
REFERENCES NETLAB代写
[1] X. Foukas, G. Patounas, A. Elmokashfifi, and M. K. Marina, “Network slicing in 5g: Survey and challenges,” IEEE Communications Magazine, vol. 55, no. 5, pp. 94–100, 2017.
[2] P. Rost, C. Mannweiler, D. S. Michalopoulos, C. Sartori, V. Sciancalepore, N. Sastry, O. Holland, S. Tayade, B. Han, D. Bega et al., “Network slicing to enable scalability and flflexibility in 5g mobile networks,” IEEE Communications Magazine, vol. 55, no. 5, pp. 72–79, 2017.
[3] D. Sattar and A. Matrawy, “Proactive and dynamic slice allocation in sliced 5g core networks,” in 2020 International Symposium on Networks, Computers and Communications (ISNCC). IEEE, 2020, pp. 1–8.
[4] H. Halabian, “Distributed resource allocation optimization in 5g virtualized networks,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 3, pp. 627–642, 2019.
[5] H. Zhang, N. Liu, X. Chu, K. Long, A.-H. Aghvami, and V. C. Leung, “Network slicing based 5g and future mobile networks: Mobility, resource management, and challenges,” IEEE Communications Magazine, vol. 55, no. 8, pp. 138–145, 2017.
[6] T. Yoo, “Network slicing architecture for 5g network,” in International Conference on Information and Communication Technology Convergence (ICTC), 2016, pp. 1010–1014.
[7] A. Kaloxylos, “A survey and an analysis of network slicing in 5g networks,” IEEE Communications Standards Magazine, vol. 2, no. 1, 60–65, 2018.
[8] Y. Lu, X. Chen, R. Xi, and Y. Chen, “An access selection mechanism in 5g network slicing,” in IEEE International Conference on Smart Internet of Things (SmartIoT), 2020, pp. 72–78. NETLAB代写
[9] V. Sciancalepore, K. Samdanis, X. Costa-Perez, D. Bega, M. Gramaglia, and A. Banchs, “Mobile traffific forecasting for maximizing 5g networkslicing resource utilization,” in INFOCOM-IEEE International Conference on Computer Communications, 2017, pp. 1–9.
[10] A. Perveen, M. Patwary, and A. Aneiba, “Dynamically reconfifigurable slice allocation and admission control within 5g wireless networks,” in IEEE 89th Vehicular Technology Conference , 2019, pp. 1–7.
[11] Y. Sun, W. Jiang, G. Feng, P. V. Klaine, L. Zhang, M. A. Imran, and Y.-C. Liang, “Effificient handover mechanism for radio access network slicing by exploiting distributed learning,” IEEE Transactions on Network and Service Management, vol. 17, no. 4, pp. 2620–2633, 2020.
[12] R. Li, Z. Zhao, Q. Sun, I. Chih-Lin, C. Yang, X. Chen, M. Zhao, and Zhang, “Deep reinforcement learning for resource management in network slicing,” IEEE Access, vol. 6, pp. 74 429–74 441, 2018.
[13] H. Wang, Y. Wu, G. Min, J. Xu, and P. Tang, “Data-driven dynamic resource scheduling for network slicing: A deep reinforcement learning approach,” Information Sciences, vol. 498, pp. 106–116, 2019.
[14] A. Thantharate, R. Paropkari, V. Walunj, and C. Beard, “Deepslice: A deep learning approach towards an effificient and reliable network slicing in 5g networks,” in IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), 2019, 0762–0767.
[15] L. Gurobi Optimization, Gurobi Optimizer Reference Manual, 2021. [Online]. Available: https://www.gurobi.com
[16] C. A. Floudas, Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications. Oxford University Press, 1995.
[17] S. Burer and A. N. Letchford, “Non-convex mixed-integer nonlinear programming: A survey,” Surveys in Operations Research and Management Science, vol. 17, no. 2, pp. 97–106, 2012.
[18] F. Glover and E. Woolsey, “Converting the 0-1 polynomial programming problem to a 0-1 linear program,” Operations Research, vol. 22, no. 1, 180–182, 1974. Authorized licensed use limited to: North China Electric Power University. Downloaded on April 02,2022 at 16:12:56 UTC from IEEE Xplore. Restrictions apply.



