MATH3049
Scientifific Computation and Numerical Analysis
Coursework 2
Numerical Analysis代写 The folder containing this fifile also contains the fifiles wave FDM.m, wave FDM problem.m, wave FVM.m, wave FVM problem.m, wave…
The folder containing this fifile also contains the fifiles wave FDM.m, wave FDM problem.m, wave FVM.m, wave FVM problem.m, wave FVM error.m, CGM.m, DLS.m and DLS problem.m. To do this coursework, you should add to these fifiles but should not rename them and should not modify the lines that are already in them. This coursework is worth 20% of your fifinal mark in this module. A penalty may be applied to your mark in this coursework for not following these instructions. The standard penalties for late submission of coursework will be applied to coursework that is submitted up to 1 week after the submission deadline. Coursework submitted more than 1 week after the submission deadline will receive a mark of 0.
You will not be penalised for not including comments or explanations in your codes. You will not be penalised for your code not being the most effiffifficient, neat or concise provided that when your code is opened in the MATLAB editor the message indicator is green (using default settings) and that your code is not ridiculously ineffiffifficient. You must not use the Symbolic Math Toolbox.
-
Consider the problem of fifinding, on [0, L] × [0, T] where L and T are positive numbers, the solution u(x, t) of the initial boundary value problem consisting of the partial difffferential equation Numerical Analysis代写
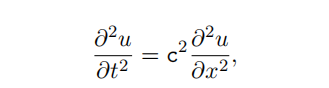
where c is a real number, with the boundary conditions
u(0, t) = u(L, t) = 0
and the initial conditions
u(x, 0) = f(x)
and
ut(x, 0) = g(x),

q entries whose ith entry is f(x(i)) for i = 1, 2, . . . , q if x is an appropriate vector with q entries, a function handle g of a function that implements g and the positive integers N and M. The wave FVM function should not print anything to the command window if the line in which it is called ends with a semicolon.
(b) Add to the fifile wave FDM problem.m to write a wave FDM problem function that calls the wave FDM function to obtain approximations to the solution u(x, t), on [0, 1] × [0, T], of the initial boundary value problem consisting of the partial difffferential equation
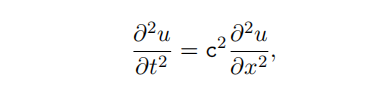
where c is a real number, with the boundary conditions Numerical Analysis代写
u(0, t) = u(1, t) = 0
and the initial conditions
u(x, 0) = sin(2πx)
and
ut(x, 0) = 0.

- Consider the problem of fifinding, on [0, L] × [0, T] where L and T are positive numbers, the solution u(x, t) of the initial boundary value problem consisting of the partial difffferential equation
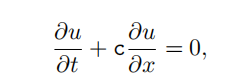
where c is a nonzero real number, with the initial condition
u(x, 0) = v(x),
where v is an appropriate function, and the boundary condition
cu(0, t) = g(t) if and only if c > 0
or the boundary condition Numerical Analysis代写
cu(L, t) = g(t) if and only if c < 0,
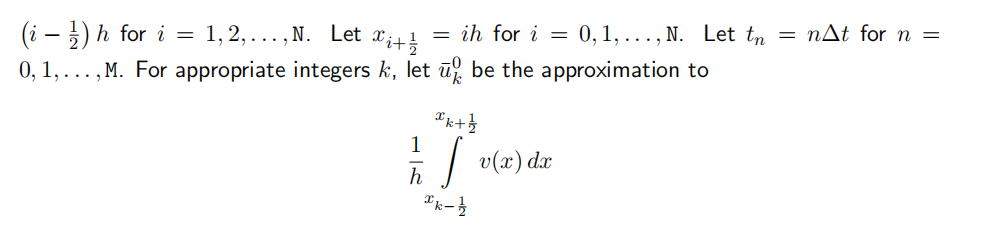
obtained using the midpoint rule for approximating integrals. A method for approximately solving the initial boundary value problem is the fifinite volume method given by

(a) Add to the fifile wave FVM.m to write a wave FVM function that returns the matrix u which has N rows and M+ 1 columns and is such that ![]() for all positive integers k which are less than or equal to N and all positive integers m which are less than or equal to M+ 1. The arguments of the wave FVM function are the positive numbers L and T, the nonzero real number c, a function handle v which is such that v(x) returns a vector with q entries whose ith entry is v(x(i)) for i = 1, 2, . . . , q if x is an appropriate vector with q entries, a function handle g of a function that implements g and the positive integers N and M.
for all positive integers k which are less than or equal to N and all positive integers m which are less than or equal to M+ 1. The arguments of the wave FVM function are the positive numbers L and T, the nonzero real number c, a function handle v which is such that v(x) returns a vector with q entries whose ith entry is v(x(i)) for i = 1, 2, . . . , q if x is an appropriate vector with q entries, a function handle g of a function that implements g and the positive integers N and M.
The wave FVM function should not print anything to the command window if the line in which it is called ends with a semicolon.
(b) Add to the fifile wave FVM problem.m to write a wave FVM problem function that calls the wave FVM function to obtain approximations to the solution u(x, t), on [0, 1] × [0, 1], of the initial boundary value problem consisting of the partial difffferential equation
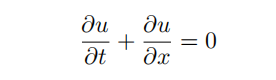
with the boundary condition Numerical Analysis代写
u(0, t) = − sin(2πt)
and the initial condition
u(x, 0) = sin(2πx).
For m = 0, 1, . . . , M, let um be such that 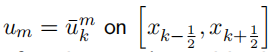 for k = 1 , 2, . . . , N. The arguments of the wave FVM problem function are the positive integers N and M and the temporal mesh size Delta t. The wave FVM problem function should not return anything. The wave FVM problem function should not print anything to the command window. The wave FVM problem function should, for m = 0, 1, . . . , M − 1, plot um inblack before pausing for Delta t seconds (subject to the accuracy of pause) and then clearing the fifigure and plotting um+1 in black, until uM has been plotted, after which the fifigure should not be cleared.
for k = 1 , 2, . . . , N. The arguments of the wave FVM problem function are the positive integers N and M and the temporal mesh size Delta t. The wave FVM problem function should not return anything. The wave FVM problem function should not print anything to the command window. The wave FVM problem function should, for m = 0, 1, . . . , M − 1, plot um inblack before pausing for Delta t seconds (subject to the accuracy of pause) and then clearing the fifigure and plotting um+1 in black, until uM has been plotted, after which the fifigure should not be cleared.
The horizontal axis should be labelled x and the vertical axis should be labelled u0, u1, . . . as appropriate. The horizontal axis should be labelled x and should go from 0 to 1 and the vertical axis should be labelled u0, u1, . . . , uM as appropriate and should go from ![]() The wave FVM problem function should not produce more than 1 fifigure.
The wave FVM problem function should not produce more than 1 fifigure.
(c) Add to the fifile wave FVM error.m to write a wave FVM error function that calls the wave FVM function to obtain approximations to the solution u(x, t), on [0, 1] × [0, 1], of the initial boundary value problem consisting of the partial difffferential equation
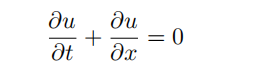
with the boundary condition
u(0, t) = − sin(2πt)
and the initial condition
u(x, 0) = sin(2πx)
for N = 21, 22 , . . . , 2p and M = N. The FVM error function should plot a loglog plot of
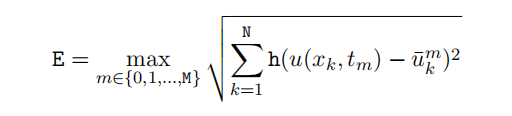
for all of the values of the mesh size h = ∆t that correspond to the values of N and M for which you were asked to compute approximations. The horizontal axis should be labelled mesh size and the vertical axis should be labelled E. The argument of the wave FVM error function is the positive integer p. The wave FVM error function should not return anything. The wave FVM error function should not produce more than 1 fifigure. Consider the question: Once h and ∆t are suffiffifficiently small. By approximately what factor is the error E reduced each time h and ∆t are halved?
Answer this question in the fifile wave FVM error in such a way that your answer is printed to the command window as a result of the command help wave FVM error. The wave FVM error function should not print anything to the command window except as a result of the command help wave FVM error. Note that
u(x, t) = sin(2π(x − t)).
[30 marks]
-
(a) Add to the fifile CGM.m to write a CGM function that returns an approximation to the solution g of Ag =b obtained using the conjugate gradient method with an initial approximation of the appropriate zero vector. The arguments of the CGM function are an appropriate symmetric positive defifinite matrix A. And an appropriate column vector b, a positive real number tol and a positive integer maxits. Iterations should be performed until the 2-norm of the residual vector is less than the tolerance tol if such an approximation can be found without performing more than maxits iterations. Numerical Analysis代写
An appropriate message should be printed to the command window if maxits iterations have been performed. And the 2-norm of the residual vector is still not less than tol. The CGM function should not print anything to the command window if the line in which it is called ends with a semicolon with the exception of the appropriate message mentioned above.
(b) Suppose that we have m values y1, y2, . . . , ym and m distinct points x1, x2, . . . , xm, where m is an integer that is at least 2. Let p be the polynomial of degree at most n < m − 1 which gives the best least squares fifit to this data in the sense that
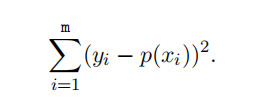
is minimised. Add to the fifile DLS.m to write a DLS script that returns the error
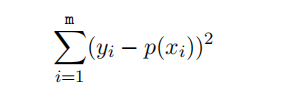
The arguments of the DLS function are a row vector x whose ith entry is xi for i = 1, 2, . . . , m, a row vector y whose ith entry is yi for i = 1, 2, . . . , m, the nonnegative integer n which is less that m − 1. And an integer fig which can be either 0 or 1 and is the number of fifigures that the DLS function should produce. If fig is 1 then the DLS function should, on the same appropriately labelled fifigure, plot p as well as the data points (xi , yi) for i = 1, 2, . . . , m. The linear system of equations that has to be solved to obtain p should be approximately solved by calling the CGM function with a tolerance of 10−13. And a maximum number of iterations of 100.
The DLS function should not print anything to the command window. If the line in which it is called ends with a semicolon with the exception of the appropriate message which could be printed by the CGM function.
(c) Consider the plot obtained by running the DLS problem script. Add comments beneath the code in the DLS problem.m fifile that describe. And explain the behaviour of the error observed in the plot with reference to the type of function that cos(πx) is.
[40 marks]



