Time Series代写 STA 137 Time Series Analysis

STA 137—Applied Time Series Analysis Solutions to Practice Problems I

Time Series代写 1.Let ∇ be the difference operator and specify the quadratic “trend” m_t = b₀ + b₂t² for some constants b_{0 and b2. What is ∇2mt?} 

1.Let ∇ be the difference operator and specify the quadratic “trend” m_t = b₀ + b₂t² for some constants b₀ and b₂. What is ∇2m_t? [Note: ∇m_t = m_t − m_t−1] Time Series代写

(a)0              (b)b₀                 (c) 2b₂t − b₂             (d) 2b₂              (e) none of the above

Note that Time Series代写

∇m_t = m_t − m_t−1

= b₀ + b₂t² − (b₀ + b₂[t − 1])²

= b₂t² − b₂[t² − 2t + 1]

= 2b₂t − b₂

2. Show that the one-sided moving average filter gives exponentially decaying weights to past observations.

Let x_t, t ∈ {1, · · · , n} be a time serise and y_t is the one-sided moving average 

y_t = ax_t + (1 − a)y_t−1,

where a ∈ (0, 1) and t ∈ {2, · · · , n}. Hence, Time Series代写

y_t = ax_t + (1 − a)y_t−1

= ax_t + (1 − a){ax_t−1 + (1 − a)y_t−2}

= ax_t + a(1 − a)x_t−1 + (1 − a)²y_t−2

.

= ax_t + a(1 − a)x_t−1 + a(1 − a)²x_t−2 + · · · + a(1 − a)^jx_t−j + (1 − a)^j+1y_t−j−1

 

It can be seen that the past observation x_t−j will be weighted with the factor a(1 − a)^j. Since 0 < a < 1, this factor decreases exponentially fast.

3. Let (Y_t : t ∈ Z) be a weakly stationary process with mean  Define the process (X_t : t ∈ Z) by letting Time Series代写

X_t = s_t + Y_t, t ∈ Z,

where (s_t : t ∈ Z) is a seasonal component of period d. Apply ∇_d to the process (X_t : t ∈ Z) and compute Cov(∇_dX_t+1, ∇_dX_t).

The operator ∇_d is defined by ∇_dX_t = X_t − X_t−d. Therefore

Cov(∇_dX_t+h, ∇_dX_t) = Cov(Y_t+h − Y_t+h−d, Y_t − Y_t−d)

= Cov(Y_t+h, Y_t) − Cov(Y_t+h, Y_t−d) − Cov(Y_t+h−d, Y_t) + Cov(Y_t+h−d, Y_t−d)

= 2γ_Y (h) − γ_Y (h + d) − γ_Y (h − d),

where γ_Y denotes the ACVF of the weakly stationary process (Y_t : t ∈ Z).

 

4. In Figure 1, n = 100 observations simulated from time series (X_t), (Y_t) and (Z_t) are  Which of the three processes is not stationary?

(a) (X_t)             (b)(Y_t)                (c) (Z_t)              (d) none of the processes is stationary

Note that the process in (c) shows an upward trend.

 

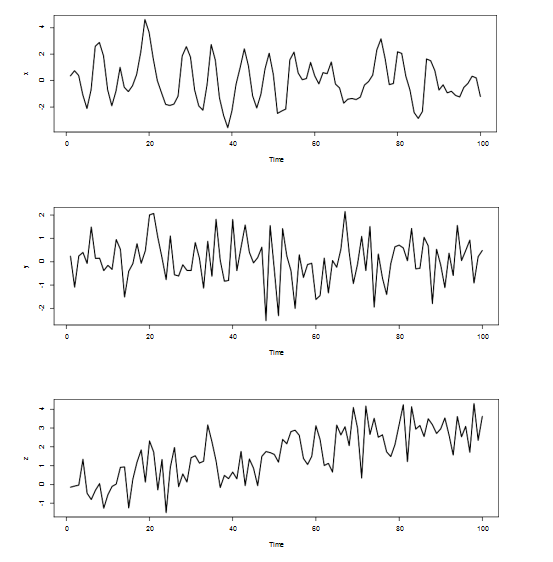
Figure 1:   Realizations of (X_t) (top), (Y_t) (middle) and (Z_t) (bottom).

 

 

5. Let(Z_t : t ∈ Z) ∼ WN(0, σ²) and let (X_t : t ∈ Z) be given by the equations Time Series代写

X_t = Z_t − Z_t−1, t ∈ Z. 

What are the values of the ACF ρ(h) = Corr(X_t, X_t+h) for h ∈ Z? Compute the ACVF first:

γ(h) = Cov(X_t, X_t+h)

= Cov(Z_t − Z_t−1, Z_t+h − Z_t+h−1)

= Cov(Z_t, Z_t+h) − Cov(Z_t, Z_t+h−1) − Cov(Z_t−1, Z_t+h) + Cov(Z_t−1, Z_t+h−1).

 

Now the properties of a WN ACVF can be exploited: contributions only appear if the time lags in the two arguments of the covariance function match. This gives

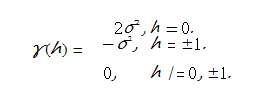
Dividing by γ(0) = 2σ² gives the ACF values Time Series代写

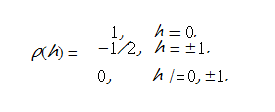
6.Let(X_t : t ∈ Z) be a stationary process with ACVF γ(h) = exp(−1.5h²) for all h ∈ Z. Give the expression for the ACF ρ(h) at lag h ∈ Z.

Observe that

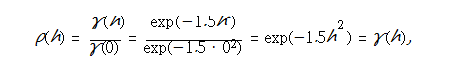
so that ACVF and ACF coincide.

7. Let(Z_t : t ∈ Z) ∼ WN(0, σ²) and let (X_t : t ∈ Z) be given by the equations Time Series代写

X_t = Z_t + 0.5Z_t−1, t ∈ Z.

Determine ρ(1). (a) 1               (b) 0.5               (c) 0.4                   (d) 0

 

Note that