Problem 1
函数代写 A ramjet propulsion system is one which produces thrust via ram compression due to a high flight speed. Essentially, the ramjet…
A ramjet propulsion system is one which produces thrust via ram compression due to a high flight speed. Essentially, the ramjet engine flies so quickly that the compressibility effects of the air alone are adequate to obtain the pressure and temperature conditions necessary to sustain combustion in the engine and produce thrust. As an exercise in functions, we shall ”march through” one of these propulsion systems – taking careful consideration to ensure that the script remains as clean and versatile as possible. In theory, a well-written script will be adaptable in such a way that you may re-purpose it later on, given different conditions.
Please note that this assignment will require you to write many new functions, thus it is highly recommended that you make sure your homework is kept neatly in a folder. To get credit for the code which you have written, you must include all of the functions in a section at the end of the script named ”Typed Functions”. In this section, simply use the ”type” command to output the contents of each function.
(a) To begin your script, please define the following variables: 函数代写
- Thealtitude in meters, z = 10000;
- Thegas constant of air in kJ/kg/K, R = 9;
- Theflight Mach number, M1 = 4;
- Thesea-level temperature in K, Ts = 288;
- Thesea-level pressure in Pa, Ps = 3*10^3;
- Thesea-level density in kg/m , rhos = 23;
- Theequivalent altitude in m, zstar = 8404;
- Theratio of specific heats, gamma = 4;
(b) Now that you have entered your givens, we shall begin the propulsion system analysis.The first function which you will make will give you the ratios of total-to-static conditions for a given Mach The equations are given as: 函数代写
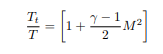
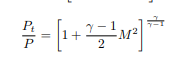
Recall that γ = ”gamma”. Using equations (1) and (2), you will build a function named TotaltoStatic to return these total-to-static relations. Your function must take gamma and M as inputs and return Tt_over_T and Pt_over_P. This function will be useful, as you will soon see. As a reminder, please realize the following:
![]()
![]()
(c) Now,you will need to create a function to calculate the standard Create a function named isenatmT which takes Ts, gamma, z, and zstar as inputs, and returns the temperature T as an output. Set the variable T1 equal to the output of this function for the given conditions. The equation for the isentropic atmospheric temperature is: 函数代写
![]()
(d) Now,you will need to create a function to calculate the standard Create a function named isenatmP which takes Ps, gamma, z, and zstar as inputs, and returns the temperature P as an output. Set the variable P1 equal to the output of this function for the given conditions. The equation for the isentropic atmospheric temperature is:
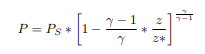
(e) Usethe values for T1 and P1 with the values returned by your Total_to_Static function to calculate the values of Pt1 and You may do this by using M1 as the input and following the algebra detailed in equations (3) and (4). Use fprintf to output the values for T1, Tt1, P1, and Pt1.
(f) Now we will create a function named SpeedSound, which will take the value of Temperature (Not tobe confused with the Total Temperature!) and compute the local speed of sound. The equation for the speed of sound is given as
![]()
Thus, by using equation (7), you may take an input value for gamma, R, and T and return the speed of sound, a. Create this function and use it to calculate the speed of sound at state 1, since you found the the value of T1 in part (c). Use fprintf to output the speed of sound at this point.
(g) Finally,by using the inlet Mach number, we may calculate the inlet velocity. Create a function named VelocityMach to do so, given the equation
V = M ∗ a
This function will take M and a (where a represents the speed of sound) and will return V, the local velocity. Use fprintf to output the velocity at this point.
Problem 2 函数代写
Aircraft performance problems tend to be very nontrivial due to the plethora of variables which may affect flight conditions. When analyzing aircraft performance, you will want to iterate through a range of altitudes and Mach numbers to understand what is going on during the various stages of flight. The Mach number, a term which you have all become rather familiar with, is a quantification of how compressible a fluid (in this case, air) is under certain conditions. Compressibility effects end up causing large changes to the performance of an aircraft, and as such, modern aircraft are able to measure the Mach number while in flight and incorporate it into their flight management systems.
In this problem, we shall march though an analysis of the Lift experienced by an aircraft wing during various flight conditions, which we will then plot.
(a) Weare interested in the flight conditions for an aircraft with dimensions similar to a Boeing To perform calculations, we shall take a few variables as given. Please define the following in your code:
- Theratio of specific heats: gamma = 4
- Thegas constant for air: R = 286 J/kg/K
- Thereference area of the wing: S = 186 m2
- Thewing aspect ratio: AR = 20
- Theuppermost Mach number: Mach_Limit = 82
(b) Wehave provided an excel document containing atmospheric data for the range of flight conditions that you are interested in analyzing. Import this dataset using [ALT, P, T, rho] = readvars(’StdAt.xlsx’);. This data supplements the isentropic atmosphere approximation which you made in Problem 1.

(c) We want to test the flight conditions at a number of altitudes and Mach You need to generate a vector named ”MACH” and have it span the range of [0.2, Mach_Limit] in increments of 0.02. Do this by saying MACH = 0.2:0.02:Mach_Limit. Once you have completed this, you must generate a vector of lift coefficients for the finite wing section. This is given empirically as 函数代写
CL ≈ 0.1261 ∗ MACH2 − 0.039 ∗ MACH + 0.1719
Call this variable CL. You may complete this using element-wise array operations, there is no need for a for-loop.
(d) Before starting your double-nested for-loop, you need to initialize three arrays:V, q_inf, and L. The meaning of these variables will soon become apparent. To initialize, use the zeros command. You want the rows dimension of the array to correspond with the altitude and the columns dimension to corre- spond with the Mach number. Do this with <VARIABLE NAME> = zeros(length(ALT),length(MACH)), replacing <VARIABLE NAME> with the variable you are initializing (i.e. V, q_inf, and L).
(e) Now it is time to begin your double-nested loop.Your outer loop should iterate through the al- titudes (for i = 1:length(ALT)) and the inner loop should iterate through the Mach numbers (for j = 1:length(MACH)). Inside the inner loop, you will want to calculate the velocity, given as
![]()
Remember, you must use the current value of M for the loop, and you must also use the T value which corresponds to the altitude you are at. Thus, this equation will look like the following, in MATLAB:
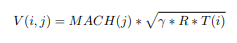
Recall that γ ”gamma”. Using this velocity, calculate the dynamic pressure. Again, you need to use the current velocity that you have calculated for each combination of Mach and Altitude. 函数代写
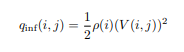
Recall that ρ ”rho”. Finally, using this value of q inf, you may calculate the lift for the aircraft using the following equation:
L(i, j) = CL(j) ∗ qinf(i, j) ∗ S
Again, ensure you are using the CL value corresponding to the Mach number. This is the last calculation you will need inside your loop. We have provided the indicies, to simplify the equations in your code. Although we have given the indicies, please take some time to understand how the for-loop is iterating through things, as it will help you better understand the underlying processes.
(f) Using a contour plot, show the trends with the amount of lift generated as a function of Mach and The command to use is contour(MACH,ALT,L,5,’k’,’ShowText’,’on’). Use the xlabel and ylabel commands to name the axes ”Mach” and ”Altitude (m)”, respectively. Give the plot an appropriate title using the title() command, as well.
To validate your code: 函数代写
- Thevector for Mach should be a ”1×32 double” in the workspace.
- The array for ”L” should show as a ”35×32 double”. If this is not the case, check your bounds in the for-loops
- When you plot your values, you should see the lift increasing as the Mach number increases, but decreasing as the altitude increases. Your absolute maximum lift should be in the range of 1,500,000- 2,000,000 N.



