MAT 3120, Fall 2019 – Final Exam
Final Exam代考 Cellular phones, electronic devices (including calculators) or course notes are not allowed during this exam. Phones and…
Read the following instructions: Final Exam代考
- Cellular phones, electronic devices (including calculators) or course notes are not allowed during this exam. Phones and devices must be turned offff and put away in your bag. Do not keep them in your possession, such as in your pockets. If caught with such a device or document, the following may occur: academic fraud allegations will be fifiled which may result in your obtaining a 0 (zero) for the exam.
- This is a closed book exam containing 6 questions plus a bonus question.
- There is an additional blank page at the end of this exam that you may use as scrap paper. If you run out of space, you may use this page or the back of pages. Clearly indicate where to fifind your answer.
- Do not detach the pages of this test, apart from the last (blank) page. If you detach the last page, do not use it for your submitted answers.
- You must give clear and complete solutions, with calculations, explanations and justififi-cations. Make sure that your answer is clearly indicated; you must convince me that you understand your solution in order to receive full marks.
By signing below, you acknowledge that you are required to respect the above statements. Final Exam代考
- Let V, W be normed vector spaces and let T : V → W be a linear map.
(a) Prove that if T is continuous then there exists M > 0 such that
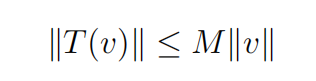
for all v ∈ V . 10
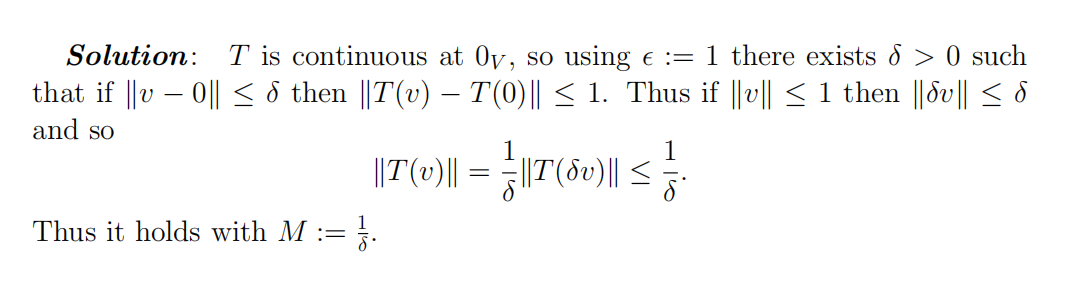
(b) Prove the converse: if there exists M > 0 such that
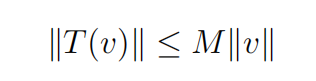
for all v ∈ V , then T is continuous. 10
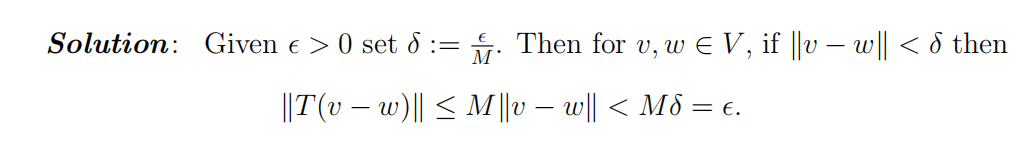
This shows that T is (uniformly) continuous.MAT 3120, Fall 2019, December 7, 2019, 14:00-17:00 3
- Let X, Y be metric spaces and let f : X → Y be a function.
(a) Prove that f is continuous if and only if for every open set U ⊆ Y , f−1(U) is open in X. 10 Final Exam代考
Solution: ⇒: Let U ⊆ Y and let x ∈ f−1(U). Then f(x) ∈ U and since U is open, there exists > 0 such that B(f(x), ) ⊆ U. Since f is continuous at x,
there exists δ > 0 such that f(B(x, δ)) ⊆ B(f(x), ). Thus B(x, δ) ⊆ f−1(U), as required.
⇐: Let x ∈ X and let > 0. Set U := B(f(x), ), which is open. Therefore by hypothesis, f−1(U) is open. Since x ∈ f−1(U), there exists δ > 0 such that
B(x, δ) ⊆ f−1(U). This means that f(B(x, δ)) ⊆ U = B(f(x), ), as required.
(b) Is it true that if f is continuous then if for every open set U ⊆ X, f(U) is open in Y ? Give a proof or counterexample. 5
Solution: No. Let f : R → R be given by f(x) := 0. Then R is open but f(R) = {0} is not.
(c) What about the converse – if for every open set U ⊆ X, f(U) is open in Y , does it follow that f is continuous? Give a proof or counterexample. 5

- Let X be a metric space.
(a) Defifine what it means for a subset A ⊆ X to be open. 4
Solution: See notes.
(b) Defifine what it means for a subset A ⊆ X to be dense. 4
Solution: See notes.
(c) Prove that if U1, . . . , Un ⊆ X are each dense and open, then their intersection, Final Exam代考
U1 ∩ · · · ∩ Un
is also dense. (Note that you cannot use the Baire Category Theorem, since X might not be complete.) 12
Solution: U1 ∩ U2 is open since it is the intersection of open sets. So, by induction, it suffiffiffices to prove that U1 ∩ U2 is dense.
Let x ∈ X and let > 0. Then B(x, ) ∩ U1≠∅ since U1 is dense. This set is also open, so there exists δ > 0 such that B(x, δ) ⊆ B(x, ) ∩ U1.
Since U2 is dense, B(x, δ) ∩ U2≠∅. Thus,
∅ ≠ B(x, δ) ∩ U2 ⊆ B(x, ) ∩ U1 ∩ U2,
as required.
- Let X be a metric space.
(a) Defifine what it means for X to be compact. (Do not defifine sequential compactness.) 5
Solution: See notes.
(b) Prove that if X is compact then it is sequentially compact. 15 Final Exam代考
Solution: Let {xn}∞n=1 be a sequence. Suppose for a contradiction that it no subsequence converges, so for every a ∈ X, there exists a > 0 and Na such that d(xn, a) ≥ x for all n ≥ Na.
Then {B(a, a) : a ∈ X} forms an open cover for X, and so by compactness there is a fifinite subcover indexed by a1, . . . , ak. Take n ≥ max{Na1 , . . . , Nak }. Then since X = B(a1, a1 ) ∪ · · · ∪ B(ak, ak ), we must have xn ∈ B(ai , ai ) for some i. But since n ≥ Nai , this is a contradiction.MAT 3120, Fall 2019, December 7, 2019, 14:00-17:00 7
- Let V be a Hilbert space and let T : V → V be a bounded linear operator.
(a) Defifine the operator T∗ . (You do not need to prove that it exists/is well defifined.) 5
Solution: See notes.
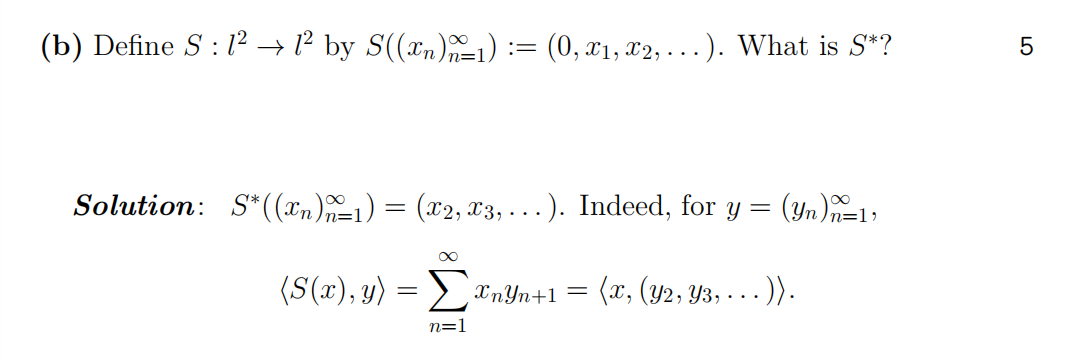

- In this question C([0, 1]) denotes the normed vector space of continuous functions [0, 1] → R, equipped with the norm k fk ∞ := supx∈[0,1] |f(x)|.
(a) Let T : C([0, 1]) → R be a bounded linear map, such that for any polynomial function p(x) := a0 + a1x + · · · + pkxk,
T(p) = a0.
Prove that T(f) = f(0) for all f ∈ C([0, 1]). 15 Final Exam代考
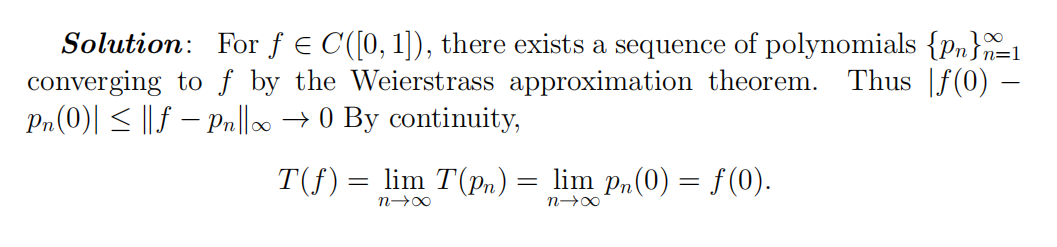
(b) Does there exist a bounded linear map S : C([0, 1]) → R such that for any polynomial function p(x) := a0 + a1x + · · · + pkxk, S(p) = a1? 5

- (Bonus) Let f : (0,∞) → R be a continuous function with the property that for all x ∈ (0,∞), the sequence
{f(nx)}∞n=1
converges to 0. Prove that limx→∞ f(x) = 0.
(Hint: consider the sets Fn := {x ∈ [0,∞) : |f(mx)| ≤ for all m ≥ n}. Use the Baire Category Theorem.)

Then for m ≥ n1,
mb − (m + 1)a = m(b − a) − a > a − a = 0.
This shows that the interval (ma, mb) overlaps the interval ((m+1)a,(m+1)b). Consequently, Final Exam代考
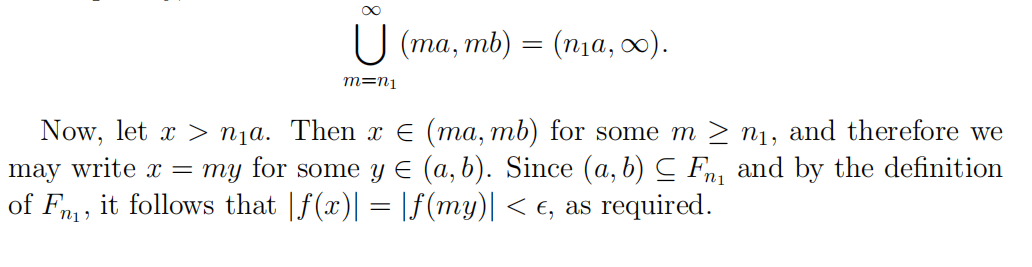
(the last page)



