MAT 3120, Fall 2019 – Midterm Exam
Midterm Exam代考 The use of cellphones, electronic devices (including calculators), and course notes is strictly forbidden. All phones and electronic devices…
Read the following instructions: Midterm Exam代考
- The use of cellphones, electronic devices (including calculators), and course notes is strictly forbidden. All phones and electronic devices must be turned offff and kept in your bags: do not leave them on you. If you are seen to have an electronic device on your person, we may ask you to leave the exam immediately, and fraud allegations could be made, which could lead to a mark of 0 (zero) on this midterm.
- This is a closed book midterm containing 4 questions. The duration is 75 minutes.
- There is an additional blank page at the end of this exam that you may use as scrap paper. If you run out of space, you may use this page or the back of pages. Clearly indicate where to fifind your answer if it is not entirely contained in the space provided on the page.
Alternatively, you may remove the last page and use it as scrap paper, but in this case, you will not be able to hand it in with your midterm.
- Apart from the fifinal (blank) page, do not detach the pages of this midterm.
- You must give clear and complete solutions, with calculations, explanations and justififi-cations. Make sure that your answer is clearly indicated; you must convince me that you understand your solution in order to receive full marks.
By signing below, you acknowledge that you are required to respect the above statements.
-
Let (X, dX), (Y, dY ) be metric spaces and let f : X → Y be a function. Midterm Exam代考
(a) Defifine what it means for f to be Lipschitz.
Solution: See notes.
(b) Prove that if f is Lipschitz and X is bounded then f(X) is bounded. 12
Solution: Let f be L-Lipschitz where L > 0, so that d(f(x), f(y)) ≤ Ld(x, y). Since X is bounded, δ(X) := sup{d(x, y) : x, y ∈ X} < ∞. Thus for w, z ∈ f(X), we can write w = f(x) and z = f(y) for some x, y ∈ X, so that d(f(x), f(y)) ≤ Ld(x, y) ≤ Lδ(X).
It follows that δ(f(X)) ≤ Lδ(X) < ∞, so that f(X) is bounded.
- Let (X, d) be a metric space.
(a) Defifine what it means for a subset U ⊆ X to be open. 6 Midterm Exam代考
Solution: See notes.
(b) Let Y ⊆ X and V ⊆ Y Prove that V is open in Y (i.e., viewing Y as its own metric space with the subspace metric) if and only if there is an open set
U of X such that V = U ∩ Y . 14
Solution: Let us use BY (x, r) to denote the open ball centred at x of radius r in the metric space Y , and BX(x, r) likewise for the metric space X. Then
when x ∈ Y , we have BY (x, r) = BX(x, r) ∩ Y .
⇒: Let V be open. Then for each x ∈ V , there exists rx > 0 such that
BY (x, rx) ⊆ V . Defifine U := S x∈V BX(x, rx). This is open in X since it is the union of open sets.
Evidently, V ⊆ U so that V ⊆ U∩X. On the other hand, since BY (x, rx) ⊆ V for each x ∈ V , we have Midterm Exam代考
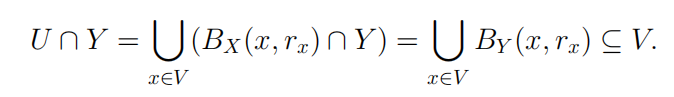
⇐: Suppose that U is an open subset of X such that V = U ∩Y . Let x ∈ V . Then since x ∈ U and U is open, there exists r > 0 such that BX(x, r) ⊆ U.
Hence, BY (x, r) = BX(x, r) ∩ Y ⊆ U ∩ Y = V , as required.
- (a) Defifine what it means for a metric space (X, d) to be separable. 5
Solution: See notes.
(b) Defifine the metric space l∞ (both the set and the metric). 5
Solution: See notes.
(c) Prove that l∞ is not separable. 10 Midterm Exam代考
Solution: Let X consist of all sequences of 0s and 1s, as a subset of l∞. If l∞ were separable, then since X is a subspace, it would also be separable (by a theorem in the lectures).
For x, y ∈ X, if x 6 = y then one of them has a 0 where the other has a 1, so d(x, y) = 1. Thus, the induced metric on X agrees with the discrete metric.
So, in order for X to be separable, it must be countable. However, X is not countable.
- Let A be set of continuously difffferentiable functions on [0, 1] and defifine d : A × A → [0,∞) by
d(f, g) := d∞(f, g) + d∞(f0 , g 0 ).
(a) Prove that d is a metric on A. 5
Solution: Symmetry is clear since d∞ is symmetric.
Since d∞ is separating on C([0, 1]) (which contains A), it follows that d is also separating.
Finally, for f, g, h ∈ A, we have
d(f, h) = d∞(f, h) + d∞(f0 , h0 )
≤ d∞(f, g) + d∞(g, h) + d∞(f0 , g 0 ) + d∞(g0 , h0 )
= d(f, g) + d(g, h).
(b) Let B := {f ∈ A : d(0, f) ≤ 1}. Prove that B is a totally bounded as a subset of (C([0, 1]), d∞). 5 Midterm Exam代考
Solution: By a theorem in the lectures, it is equivalent to prove that B is bounded in d∞ and is uniformly equicontinuous. Since d∞(0, f) ≤ d(0, f), we
see that B is bounded in d∞.
For uniform equicontinuity, let > 0 be given and set δ := . Then for f ∈ B and x, y ∈ [0, 1] satisfying |x−y| < δ, by the Mean Value Theorem, there exists z such that f(x) − f(y) = f0 (z)(x − y). Thus,
|f(x) − f(y)| = |f0 (z)| |x − y|
≤ d∞(0, f0 )|x − y|
≤ |x − y| < .
This shows uniform equicontinuity.
(c) Prove that B is not compact as a subset of (A, d). 10
Solution: Consider the mapping D : A → (C([0, 1]), d∞) given by D(f) = f0 . Evidently this mapping is 1-Lipschitz and therefore continuous. Hence if B
were compact, then D(B) would also be compact, so let us show that this is not the case.