AMATH 250 Online Assignment 7
数学online代写 Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.
Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.You may use the course materials posted on the course website and the optional text as references. You are also allowed to discuss ideas with your classmates, the course instructor and TAs. Please do not post fifinal answers or give away too much on Piazza; it will be monitored closely. Your submitted work must be written upon your own and should indicate your knowledge of the material.
Academic Integrity Declaration (AID): Fill out the Academic Integrity Declaration form and upload as a page 1 to Crowdmark. 数学online代写
I declare the following statements to be true:
- The work I submit here is entirely my own
- I have not used any unauthorized aids
- I am aware that misconduct related to examinations can result in signifificant penalties including failing the course and suspension, as outlined in Policy 71
- I have discussed the assignment with the following people (if any):
- Write your name and the date in the box below, then upload this page to Crowdmark.
Each question should be uploaded separately to Crowdmark. 数学online代写
- (a) Consider the following homogeneous linear DE;
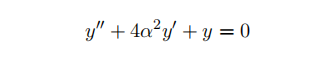
Let α be a constant. Indicate for what intervals of ↵ the system is undamped, under-damped, critically damped, and over-damped. In each case, (i) give a qualitative description of the oscillations, (ii) give an expression for the roots of the characteristic equation in terms of α – simplify as much as possible, and, (iii) state if the roots are real, imaginary or complex. For the under-damped and critically damped cases, give the full solution (in terms of α if necessary).
(b) Now consider the following nonhomogeneous linear DE;
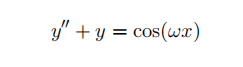
From part (a), observe that the complimentary solution naturally oscillates. Assume 0 < w < 1, fifind the solution and describe what happens to the amplitude of the oscillations as w→ 1. What does the solution become when w = 1; what happens to the amplitude?
- You need to solve the following initial value problem;
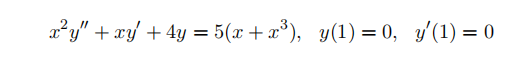
Note, however, that this is a non-homogeneous second-order linear di↵erential equation with nonconstant coeffiffifficients (which is pretty tricky). Fortunately this particular DE is not as bad as it looks. To solve it you’ll need to use some familiar tricks in (perhaps) unfamiliar ways. The following steps will guide you through the process;
(a) The homogeneous part of the DE is a Cauchy-Euler equation. To solve for the homogeneous solution, assume that x > 0, and show that the change of variable x = ez converts the DE into a constant-coeffiffifficient equation. 数学online代写
(b) Now solve the constant coeffiffifficient DE to fifind the homogeneous solution, convert this back to the original variables y and x.
(c) For the particular solution, return to the original form of the DE above, and use a polynomial trial solution to fifind a particular solution. (You could also do this with the transformed DE, but you need to transform the non-homogeneous term on the RHS above.)
(d) Finally, assemble the full solution and solve for the unknown constants using the initial conditions.




